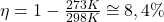Cykl Carnota

17 kwietnia, 2024 przez Karol Birecki

Cykl Carnota

Cykliczny ciąg przemian termodynamicznych zwanych cyklem Carnota dał początek rozwijaniu pojęć drugiej zasady termodynamiki, takich jak, entropia bądź sprawność maszyny termodynamicznej. To zadanie przybliża działanie tego wyidealizowanego cyklu i przedstawia podstawowy aparat matematyczny, który trafnie ilustruje zachodzenie poszczególnych przemian.

Uczniowie na zajęciach fizyki, mieli za zadanie skonstruować silnik odwzorowujący idealny cykl Carnota. Używając gazowego helu, stalowego krążka, termostatu, grzejnika, chłodnicy, izolacji termicznej i walcowej podstawy udało im się skonstruować maszynę, która schematycznie jest pokazana na rys. 1. Działała ona w trybie odwracalnych ekspansji/kompresji izotermicznych i ekspansji/kompresji adiabatycznych. Działanie tego silnika zachodziło po zamkniętym obszarze, to znaczy stan, w którym gaz się znajdował przed rozpoczęciem działania był przywracany w ostaniej przemianie.

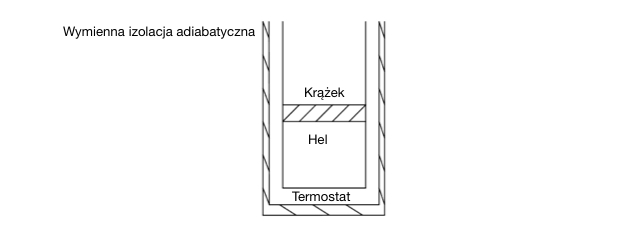
Rys. 1. Schematyczna reprezentacja urządzenia zdolnego do wykonywania cyklu Carnota. Na schemacie nie pokazano grzejnicy (kotła) ani chłodnicy.

Uwaga: Załóż, że stalowy krążek ma nieskończenie wielką właściwą pojemność cieplną, i że porusza się po walcowej podstawie bez tarcia.

Polecenia:

a. Wyprowadź wzór na pracę objętościową gazu w przemianie odwracalnej izotermicznej ekspansji/kompresji.

b. Wyprowadź relację pV dla odwracalnej przemiany adiabatycznej dla jednoatomowego gazu doskonałego (np. helu). Porównaj krzywe na wykresie pV dla przemiany izotermicznej i adiabatycznej. Podaj nierówność ostrą, która tłumaczy zmianę kształtu krzywej.

c. Wykaż, że zmiana entropii jaka zachodzi po odbyciu przez gaz jednego cyklu Carnota wynosi 0.

d. Wyprowadź wzór na pracę dla odwracalnej przemiany adiabatycznej.

e. Oblicz pracę gazu wykonaną w odwracalnym cyklu Carnota, w którym hel (1,50 mol), początkowo w temperaturze 298 K zajmował 20,0 L. Potem został on rozprężony izotermicznie do objętości 35,0 L, następnie rozprężono go adiabatycznie do temperatury 273K. Potem hel sprężony izotermicznie, został poddany adiabatycznemu sprężaniu w taki sposób, że gaz osiągnął stan pierwotny. Oblicz zmianę entropii dla każdego z tych procesów rozprężania i sprężania i wytłumacz wartość zmiany entropii dla procesu adiabatycznego.

f. Wyprowadź wzór na sprawność idealnej maszyny termodynamicznej. Oblicz sprawność cyklu przedstawionego w poleceniu e. W jaki sposób można tę sprawność zwiększyć?

Wskazówka: Sprawność maszyny termodynamicznej jest zdefiniowana jako iloraz pracy wykonanej przez maszynę i ciepła dostarczonego do maszyny.

Cykl Carnota- odpowiedzi do zadania

W rozwiązaniu zadania posłużono się podstawowym rachunkiem całkowym i różniczkowym.

aAPraca objętościowa w ujęciu termodynamiki klasycznej jest zdefiniowana jako iloczyn zmiany objętości gazu i ciśnienia, które wywołało to przemieszczenie:

$d W=-p d V$

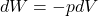
Znak minus pochodzi z konwencji. Jeżeli układ gazowy wykonuje pracę, wówczas potencjał do wykonywania kolejnej porcji pracy jest tracony, stąd energia wewnętrzna układu maleje i tak wykonana praca jest ze znakiem minus. Jeśli praca jest wykonywana w sposób quasi-statyczny (odwracalny), wówczas ciśnienie gazu wewnątrz tłoka odpowiada na każdym momencie prowadzenia procesu ciśnieniu zewnętrznemu, a proces przebiega przez nieskończoną ilość równowag mechanicznych. W takim przypadku mamy do czynienia z odwracalnym procesem ekspansji i kompresji i zgodnie z równaniem stanu gazu doskonałego można napisać:

$d W=-\frac{n R T}{V} d V$

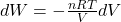
Przeprowadzając elementarne całkowanie w granicach od V₁ do V₂uzyskujemy wzór na pracę w procesie izotermicznej ekspansji/kompresji gazu doskonałego. Licznik powyższego wyrażenia jest wartością stałą w ściśle określonej temperaturze i nie jest funkcją V:

$\int_{}^{} d W=-n R T \int_{V_1}^{V_2} V^{-1} d V=-n R T \ln \frac{V_2}{V_1}$

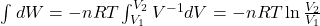
bAby poznać relację między ciśnieniem a objętością w przemianie adiabatycznej, warto najpierw określić restrykcje dotyczące wyprowadzanego równania. Po pierwsze, wiadomo że wymiana ciepła w procesie adiabatycznie izolowanym nie zachodzi. Stąd formalizm pierwszej zasady termodynamiki skraca się o składnik dQ i uzyskujemy

$dU=dW$

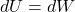
Znając definicję pracy objętościowej w procesie quasi-statycznym możemy rozwinąć:

$d U=-\frac{n R T}{V} d V=-n R T V^{-1} d V$

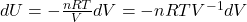
Wiedząc również, że zmiana energii wewnętrznej jest wywołana zmianą temperatury w trakcie izochorycznego ogrzewania/ochładzania podczas kompresji/ekspansji adiabatycznej można napisać:

$n C_{V} d T=-n R T V^{-1} d V$

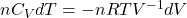
Dzieląc przez n i T uzyskujemy

$C_V T^{-1} d T=-R V^{-1} d V$

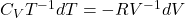
Ponownie przeprowadzając elementarne całkowanie w graniach od T₁ do T₂ oraz od V₁ do V₂dostajemy:

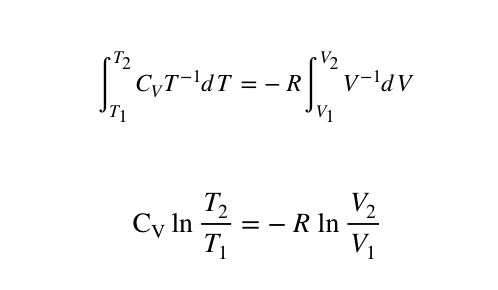
Założono tutaj, że C_V≠f(T) i że C_Vjest stałe co jest dobrym przybliżeniem w wąskich przedziałach temperatur. W rzeczywistości, rozpatrując szerokie przedziały temperatur zasadnym jest, aby uznać pojemność cieplną za funkcję temperatury. Uzyskuje się wtedy bardziej precyzyjne wyniki, ponieważ w wysokich temperaturach C_V jest stromą funkcją temperatury.

Kontynuując, jesteśmy w stanie zdelogarytmować powyższe wyrażenie kładąc obie strony równania jako wykładnik liczby e

$e^{C_{V} \ln \frac{T_{2}}{T_{1}}}=e^{-R \ln \frac{V_{2}}{V_{1}}}$

$\left(\frac{T_{2}}{T_{1}}\right)^{C_{V}}=\left(\frac{V_{2}}{V_{1}}\right)^{-R}$

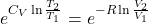
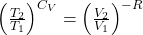
W tym momencie, wiedząc z równania stanu, że T=pV/nR, można położyć taki iloraz zamiast temperatury aby uzyskać relację między ciśnieniem a objętością gazu w przemianie adiabatycznej.

Wówczas

$\left[\frac{\frac{p_{2} V_{2}}{n R}}{\frac{p_{1} V_{1}}{n R}}\right]^{C_{V}}=\left(\frac{V_{2}}{V_{1}}\right)^{-R}$

$\left(\frac{p_{2} V_{2}}{p_{1} V_{1}}\right)^{C_{V}}=\left(\frac{V_{1}}{V_{2}}\right)^{R}$

$\left(p_{2} V_{2}\right)^{C_{V}}=\left(\frac{V_{1}}{V_{2}}\right)^{R}\left(p_{1} V_{1}\right)^{C_{V}}=V_{1}^{C_{V}+R} V_{2}^{-R}p_{1}^{C_{V}}$

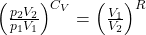
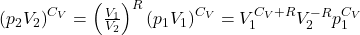
Wiedząc, że C_P-C_V=R można zamienić sumę w wykładniku V₁ na C_pi zastosować to samo wyrażenie w dalszych przekształceniach.

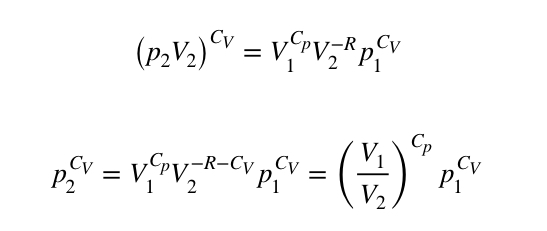
Podnosząc obie strony równania do potęgi 1/C_V:

$p_{2}=\left(\frac{V_{1}}{V_{2}}\right)^{\frac{C_{p}}{C_{V}}} p_{1}$

$\frac{C_{P}}{C_{V}}=\gamma$

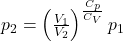
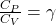
Stąd uzyskujemy finalny wynik

$p_{2} V_{2}^{\gamma}=p_{1} V_{1}^{\gamma}$

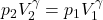
Wiedząc, że w przemianie adiabatycznej, quasi-statycznej ekspansji gaz się ochładza, można przewidzieć, że tempo spadku ciśnienia w takiej przemianie będzie większe niż w przemianie izotermicznej, gdzie dT=0. Wiedząc ponadto, że współczynnik adiabaty, gamma, jest zawsze większy od 1, można stwierdzić, że adiabata będzie bardziej stromą krzywą niż izoterma. Ilustruje to poniższy rysunek który porównuje graficznie izotermę z adiabatą.

Widać, że te krzywe w pewnym punkcie się przecinają. Zielona krzywa ilustruje izotermę, niebieska zaś adiabatę. Wykresy zostały pokazane na przykładzie jednoatomowego gazu doskonałego, gdzie współczynnik adiabaty wyniósł 5/3. Na osi odciętych umieszczono objętość, a ciśnienie na osi rzędnych. γ>1.

Komentarz: Na powyższym rysunku adiabatą jest równanie p=nRTV^(-γ) dla T=300 K, n=1 mol oraz R=8,314 J mol^-1K^-1. Wstawienie T jako wartości stałej było zasadne, ponieważ proces adiabatycznej ekspansji można rozpatrywać jako złożenie dwóch procesów. Pierwszym jest izotermiczna ekspansja, drugim z kolei izochoryczne ochładzanie. Podczas izotermicznej ekspansji, układ nie pobiera ciepła (jest odizolowany adiabatycznie) stąd musi zajść zmiana (spadek) temperatury gazu. Ochładzanie to zostało uwzględnione w powyższym wyprowadzeniu i relacja p∝V^(-γ) trzyma w mocy.

cWykazanie tej zależności jest tożsame z udowodnieniem, że entropia jest w istocie funkcją stanu. Ogólnie, właściwością funkcji stanu jest brak jej zmiany w przemianach zachodzących w silnikach (cyklach). Przykładem jest wspomniany w zadaniu cykl Carnota (czyt. cykl Karno). Można tą zależność pokazać ogólnie dla arbitralnie obranej funkcji stanu:

$\oint_{i}^{f} d Z = 0$

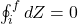
Gdzie Z reprezentuje dowolną funkcję stanu taką jak na przykład entalpia bądź energia swobodna. Powyższe wyrażenie oznacza, że sumowanie nieskończenie małych zmian jakich doświadcza funkcja Z w trakcie zachodzenia każdej przemiany termodynamicznej po zamkniętej drodze (cyklu), gdzie droga się zaczyna w punkcie i i kończy w punkcie f, wynosi 0. Dla naszego przypadku, wyrażenie ogólne przyjmie postać:

$\oint_{i}^{f} d S = 0$

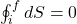
Gdzie i symbolizuje punkt, w którym ekspansja izotermiczna znajduje swój początek, a f punkt zakończenia adiabatycznej kompresji. Nietrudno jest zaobserwować, że punkty te są tożsame. Równie dobrze można było napisać:

$\oint d S = 0$

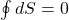
Jednak opatrzenie symbolu całki indeksami wskazującymi początek oraz koniec drogi daje obrazowe spojrzenie na to, jakim zmianom dana funkcja stanu podlega.

Początek dowodu da obserwacja, że w adiabatach wymiana ciepła z otoczeniem nie zachodzi, stąd iloraz dQ/T jest równy zero. Wypływa stąd oczywisty wniosek, że adiabata jest izoentropą (dla przemian odwracalnych, quasi-statycznych). Następnie, możemy spojrzeć w jakich procesach entropia się zmienia. Naturalnym jest, iż entropia zmienia się w przemianach izotermicznych ekspansji/kompresji.

Aby nadać ścisły charakter dowodowi, wprowadźmy następującą symbolikę:

V₁-objętość początkowa próbki gazu (początek ekspansji izotermicznej)

V₂-objętość po ekspansji izotermicznej (początek ekspansji adiabatycznej)

V₃-objętość po ekspansji adiabatycznej (początek kompresji izotermicznej)

V₄-objętość po kompresji izotermicznej (początek kompresji adiabatycznej)

Droga V₄→V₁więc zamyka cykl.

W kompresji/ekspansji izotermicznej, energia wewnętrzna układu się nie zmienia

$\left(\frac{\partial U}{\partial V}\right)_{T}=\pi_{T}=0$

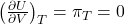
traktujemy układ jak złożony z gazów doskonałych, stąd praca wykonana w ekspansji ma taką samą wartość jak ciepło wymienione z otoczeniem z przeciwnym znakiem:

$d W=-d Q$

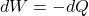
Z wyprowadzanego w punkcie a równania możemy wstawić

$-d Q=-n R T \ln \frac{V_{2}}{V_{1}}$

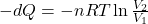
Ponadto znając wzór definiujący entropię (dS=dQ/T) można wstawić powyższe wyrażenie w licznik wzoru definicyjnego

$\Delta S=\frac{n R T \ln \frac{V_{2}}{V_1}}{T}=n R \ln \frac{V_{2}}{V_{1}}$

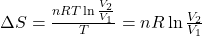
Znak delta pojawia się dlatego, że wyrażenie na ciepło zostało scałkowane. (ΔS=∫dS, w arbitralnie obranych granicach).

Można zaimplementować to równanie, aby móc wyrazić zmianę w entropii po przejściu z punktu 1, do punktu 2 (ekspansja izotermiczna):

$\Delta_{1 \rightarrow 2} S=n R \ln \frac{V_{2}}{V_{1}} V_{2}>V_{1}$

Analogicznie, przejście od 3 do 4 można opisać następująco:

$\Delta_{3 \rightarrow 4} S=n R \ln \frac{V_{4}}{V_{3}} V_{4}<V_{3}$

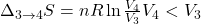
Aby więc wykazać, że zmiana entropii w całym układzie jest równa zero po przebyciu przez gaz pełnego cyklu, suma zmian drogi 1→2 oraz drogi 3→4 musi być równa zero. Zważywszy na to, że iloczyn nR jest stały, należy pokazać, że stosunek objętości gazów przed i po kompresjami i ekspansjami izotermicznymi jest taki sam. Innymi słowy, trzeba pokazać że krotność wzrostu objętości w ekspansji jest równa co do wartości krotności spadku objętości w kompresji. Na przykład, jeżeli gaz ekspanduje 2-krotnie w drodze 1→2, to musi kompresować się 2-krotnie na drodze 3→4. Tylko wtedy suma entropii poszczególnych dróg będzie równą zeru. Można tego łatwo dowieść przywołując relację między T a V w przemianie adiabatycznej (wyprowadzenie z punktu b):

$V_{2} T_{1}^{C}=V_{3} T_{2}^{C} V_{4} T_{2}^{C}=V_{1} T_{1}^{C} C=constant$

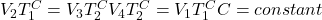
Łącząc oba równania ze sobą uzyskujemy:

$V_{2}V_{4}T_{1}^{C}T_{2}^{C}=V_{1}V_{3}T_{1}^{C}T_{2}^{C}$

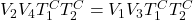
Po skróceniu iloczynu temperatur i podzieleniu na krzyż objętości dostajemy

$\frac{V_{1}}{V_{2}}=\frac{V_{4}}{V_{3}}$

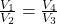
Mając to wyrażenie możemy przejść do finalnego kroku czyli sumowania zmian entropii:

$\Delta S=\Delta_{1 \rightarrow 2} S+\Delta_{3 \rightarrow 4} S=n R \ln \frac{V_{2}}{V_{1}}+n R \ln \frac{V_{4}}{V_{3}}=n R\left(\ln \frac{V_{2}}{V_{1}}+\ln \frac{V_{4}}{V_{3}}\right)$

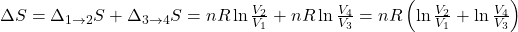
Jak wiadomo V₄/V₃ równa się V₁/V₂i można podstawić tą zależność do drugiego logarytmu w powyższym równaniu uzyskując

$\Delta S=n R\left(\ln \frac{V_{2}}{V_{1}}+\ln \frac{V_{1}}{V_{2}}\right)=nR \ln \frac{V_{2} V_{1}}{V_{1} V_{2}}=n R \ln 1=0$

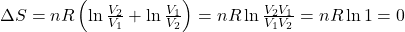
Co kończy dowód.

d.Znając relację między ciśnieniem a objętością w przemianie adiabatycznej, wyprowadzenie tej relacji nie powinno sprawić kłopotów. Mianowicie wiadomo, że na każdym etapie procesu adiabatycznego spełniona jest równość pV^γ=p₁V₁^γ, tak więc do wzoru definiującego pracę objętościową (dW=-pdV), można wstawić za p człon p₁V₁^γ/V^γi scałkować je w odpowiednich granicach, powiedziawszy to

$d W=-p d V=-\frac{p_{1} V_{1}^{\gamma}}{V^{\gamma}} d V$

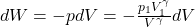
W tym miejscu należy przeprowadzić elementarne całkowanie w graniach od V₁do V₂, zgodnie z definicją pracy objętościowej

$W=-\int_{V_{1}}^{V_{2}} \frac{p_{1} V_{1}^{\gamma}}{V^{\gamma}} d V=-p V_{1}^{\gamma} \int_{V_{1}}^{V_{2}} V^{-\gamma} d V-p_{1} V_{1}^{\gamma}\left(\frac{V_{2}^{-\gamma+1}}{1-\gamma}-\frac{V_{1}^{-\gamma+1}}{1-\gamma}\right)$

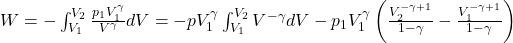
Następnie, mnożąc nawias przez czynnik znajdujący się przed nawiasem:

$W=-\frac{p_{1} V_{1}^{\gamma} V_{2}^{-\gamma+1}}{1-\gamma}+\frac{p_{1} V_{1}^{\gamma}V_{1}^{-\gamma-1}}{1-\gamma}$

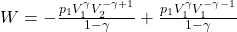
Wykonując dodawanie wykładników na prawym członie wyrażenia i podstawiając p₁V₁^γ=p₂V₂^γdostajemy

$W=\frac{-p_{2} V_{2}^{\gamma} V_{2}^{-\gamma+1}+p_{1} V_{1}}{1-\gamma}=\frac{p_{1} V_{1}-p_{2} V_{2}}{1-\gamma}$

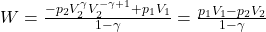
Warto zauważyć, że w procesie adiabatycznym praca wykonana jest równa zmianie energii wewnętrznej U więc tożsame wyrażenie można byłoby uzyskać rozpatrując zmianę temperatury w procesie adiabatycznym:

$d U=d W=n C_V dT$

$W=n \int_{T_{1}}^{T_{2}} C_{V} d T$

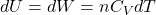
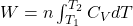
Znając postać funkcji C_V=f(T) dla danego gazu możemy to równanie łatwo rozwiązać. Jeżeli uznamy, że C_V nie zależy od temperatury wówczas ponownie traktujemy pojemność cieplną jako wyraz stały:

$W=n C_{V} \int_{T_{1}}^{T_{2}} d T=n C_{V}\left(T_{2}-T_{1}\right)$

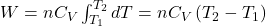
Pamiętając, że to uproszczenie jest zasadne jedynie w wąskich przedziałach temperatury.

ePrawidłowe wyprowadzenie powyższych równań da początek rozwiązaniu podpunktu e.

1) Izotermiczna ekspansja

$W=-1,5 \cdot 298 \cdot 8,314 \cdot \ln \frac{35}{20}=-2080 \mathrm{~J}$

$\Delta_{1 \rightarrow 2} S=1,5 \cdot8,314 \cdot \ln \frac{35}{20}=+6,98 \mathrm{~J} \mathrm{~K}^{-1}$

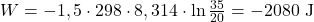
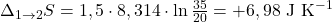
2) Adiabatyczna ekspansja

$Q=0=\Delta_{2 \rightarrow 3} S$

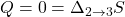
Jako iż nie ma wymiany ciepła z otoczeniem, a proces jest odwracalny, entropia nie ulega zmianie.

Pracę można obliczyć dwojako. Pierwszym sposobem korzystając z zależności od temperatury lub znając ciśnienia i objętości przed i po ekspansji. Zaprezentuję dwa sposoby i pokażę, że są one ekwiwalentne.

Temperatura

Wiedząc, że Hel jest gazem jednoatomowym, można przywołać zasadę ekwipartycji energii i przewidzieć jego izochoryczną pojemność cieplną równą 3/2R. Kontynuując, jego izobaryczna pojemność cieplna wynosi 5/2R. Znając temperaturę początkową oraz końcową:

$W=1,5 \cdot \frac{3}{2} \cdot 8,314 \cdot \int_{298}^{273} d T=-467 \mathrm{~J}$

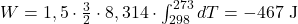
(Zamiast kłaść dolną granicę całki jako większą, można było położyć znak minus przed wyrażeniem i uzyskać ten sam wynik).

Ciśnienie i objętość

Objętość końcową policzę z poniższej zależności (zachęcam do samodzielnego wyprowadzenia tego wzoru):

$V_{2}=V_{1}\left(\frac{T_{2}}{T_{1}}\right)^{\frac{1}{1-\gamma}}$

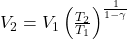
Stąd dostaję V₂=39,9 L

$p_{1}=\frac{n R T_{1}}{V_{1}}=\frac{298 \cdot 8,314 \cdot 1,5}{0,035}=1,06 \cdot 10^{5} \mathrm{~Pa}$

$p_{2}=\frac{n R T_{2}}{V_{2}}=\frac{1,5 \cdot 8,314 \cdot 273}{0,0399}=8,53 \cdot 10^{4} \mathrm{~Pa}$

$W=\frac{p_{1} V_{1}-p_{2} V_{2}}{1-\frac{\frac{5}{2} R}{\frac{3}{2} R}}=\frac{p_{1} V_{1}-p_{2} V_{2}}{1-\frac{5}{3}}=\frac{0,035 \cdot 1,06 \cdot 10^{5}-8,53 \cdot 10^{4} \cdot 0,0399}{1-\frac{5}{3}}=-460J$

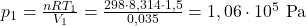
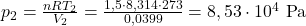
Komentarz: Odchylenie o +7J jest spowodowane zaokrągleniem wartości ciśnień wziętych do obliczeń- obliczanie związane z uwzględnieniem zmiany wyłącznie w temperaturze owocuje w bardziej rzetelny wynik pomimo, że oba sposoby są tożsame. Jest to spowodowane dużą ilością cyfr po przecinku w wartościach pośrednich ciśnień.

3) Adiabatyczna kompresja

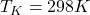$T_K=298 K$ (temperatura po kompresji)

$V_2=20L$

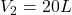
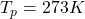$T_p=273K$ (temperatura przed kompresją)

$V_1=20 \cdot\left(\frac{298}{273}\right)^ \frac{1}{\frac{5}{3}-1}=22,8L$

$W=\frac{p_{1} V_{1}-p_{2} V_{2}}{1-\gamma}=\frac{n R T_{1}-n R T_{2}}{1-\gamma}=\frac{1,5 \cdot 8,314 \cdot 273-1,5 \cdot 8,314 \cdot 298}{1-\frac{5}{3}}=+468J$

$\Delta S=0$

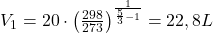
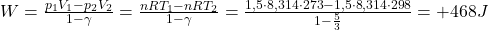
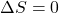
Komentarz: Warto zwrócić uwagę na wartości pracy wykonanej przez układ i wykonane na układzie podczas kompresji i ekspansji. W rzeczywistości są to wartości równe i przeciwne co do znaku (bo jak wyżej dowiedziono, krotność ekspansji jest taka sama jak krotność kompresji). Odstępstwa są spowodowane zaokrągleniami wyników pośrednich.

4) Kompresja izotermiczna

$V_{K}=22,8 L$
$V_{p}=39,9 L$

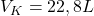
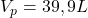
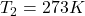$T_{2}=273 K$ (nie ulegnie zmianie, została uwzględniona aby unaocznić obniżenie temperatury z 298 K w adiabatycznej ekspansji)

$\Delta S=1,5 \cdot 8,314 \cdot \ln \frac{22,8}{39,9}=-6,98JK^{-1}$
$W=-1,5 \cdot 8,314 \cdot 273 \cdot \ln \frac{22,8}{39,9}=+1905 J$

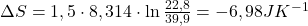
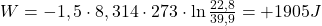
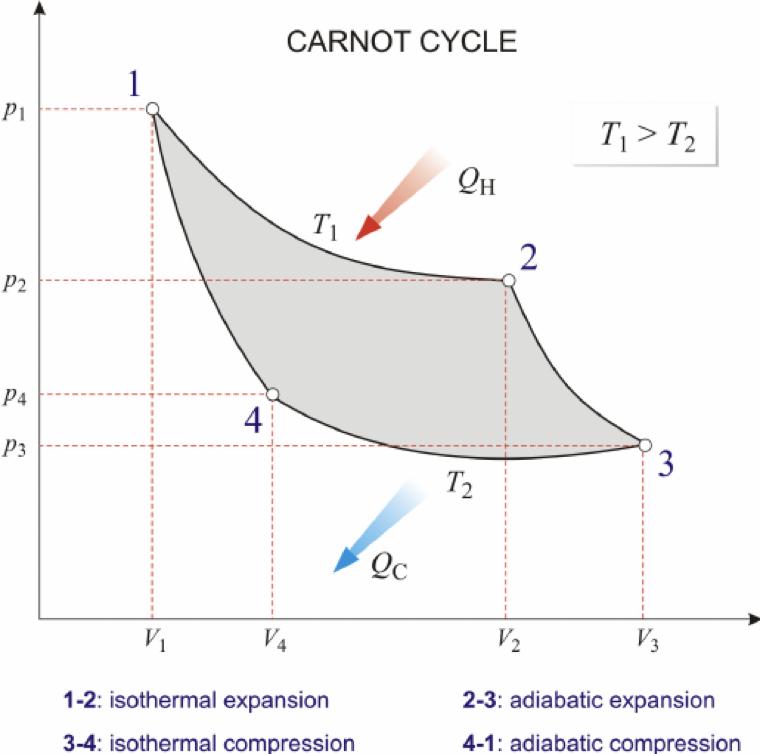
Poniższy rysunek ilustruje cykl Carnota[1]. Zacienione pole reprezentuje pracę wykonaną przez gaz w całym cyklu. Czerwona strzałka pokazuje proces, w którym gaz pobiera ciepło od grzejnicy, niebieska strzałka zaś pokazuje ciepło oddawane przez gaz do chłodnicy.

[1] Araceli, & Venegas-Gomez, Araceli. (2014). The Thermodynamics of the living organisms: entropy production in the cell. 10.13140/2.1.1573.7284.

Aby uzmysłowić sobie pojęcie pracy w cyklu Carnota, można pomyśleć o niej jak o powierzchni. Powyższy rysunek dobrze oddaje to koncepcyjnie. Mianowicie, zaciemnione pole uzyskamy kiedy poddamy gaz ekspansji izotermicznej, następnie dodamy „pole” uzyskane przez ekspansję adiabatyczną i dodamy te pola do siebie. Wtedy mamy pole, które „dotyka” osi V i nie jest to wartość pracy wykonanej. Rzeczywistą wartość pracy uzyskamy gdy od tego pola uzyskanego przez zsumowanie pracy w izotermie i adiabacie odejmiemy pole kompresji izotermicznej i adiabatycznej. Wtedy końcowo, na diagramie pV pozostaje jedynie ten mały wycinek, który stanowi pole szare. Można to dobrze, oddać matematycznie, pamiętając że pole nie może być ujemne dlatego warto posłużyć się wartościami bezwzględnymi pracy |W|.

f.Wiedząc, że całka oznaczona reprezentuje pole powierzchni ograniczone daną krzywą możemy wykorzystać scałkowane równania na pracę i dodawać je do siebie jak pola powierzchni.

$W_{\text {carnot }}=\left|W_{1}\right|+\left|W_{2}\right|-\left|W_{3}\right|-\left|W_{4}\right|$

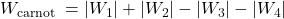
Gdzie indeks dolny pokazuje, którego procesu dotyczy dana praca (dla przypomnienia: 1-ekspansja izotermiczna, 2-ekspansja adiabatyczna, 3-kompresja izotermiczna, 4-kompresja adiabatyczna).

Przywołując scałkowane równania na pracę dostajemy:

$W_{\text {carnot }}=\left|-n R T_1 \ln \frac{V_{2}}{V_{1}}\right|+\left|n C_{V}\left(T_{2}-T_{1}\right)\right|-|-n R T_{2} \ln \frac{V_{4}}{V_{3}}|-| n C_{V}\left(T_{1}-T_{2}\right) \mid$

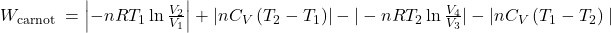
Porządkując, i pamiętając, że V₁/V₂=V₄/V_3,dostajemy:

$W_{\text {carnot }}=n R \ln \frac{V_{2}}{V_{1}}\left(T_{1}-T_{2}\right)$

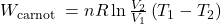
Wiedząc, że gaz czerpie ciepło w procesie izotermicznej ekspansji, możemy zdefiniować sprawność maszyny termodynamicznej jako iloraz pracy wykonanej w danym cyklu i ciepła przyłożonego aby tą pracę wykonać:

$\eta=\frac{W_{carnot}}Q =\frac{n R \ln \frac{V_{2}}{V_{1}}\left(T_{1}-T_{2}\right)}{n R T_{1} \ln \frac{V_{2}}{V_{1}}} =\frac{T_{1}-T_{2}}{T_{1}}=1-\frac{T_{2}}{T_{1}} \Leftrightarrow T_{2}<T_{1}$

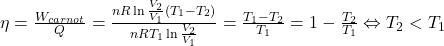
Z powyższego stwierdzenia wynika, że sprawność maszyny termodynamicznej, nawet wyidealizowanej, nie osiągnie 100%. Można to przewidzieć na gruncie trzeciej zasady termodynamiki, która mówi, że osiągnięcie temperatury 0 w skali temperatury termodynamicznej nie jest możliwe. Najniższa odnotowana temperatura na planecie Ziemia wyniosła 38 pK (pikokelwinów).

Aby zwiększyć sprawność można starać się zmniejszać maksymalnie temperaturę chłodnicy oraz jednocześnie podwyższyć temperaturę (potencjał termiczny) kotła, tak aby wartość ilorazu dążyła do zera.

W naszym cyklu:

$\eta=1-\frac{273 K}{298 K} \cong 8,4 \%$

Post Views: 2 192

Komentarze |0|

Anuluj

Legenda *) Pola oznaczone gwiazdką są wymagane
**) Możesz używać tych znaczników i atrybutów HTML:

<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

Cykl Carnota

Komentarze |0|

Anuluj

Zapisz się do naszego newslettera!

Kategorie