Kinetyka rozpadów promieniotwórczych
Zapraszam do kolejnego wpisu o kinetyce! Jeśli nie spotkał*ś się jeszcze wcześniej z tym działem, polecam zajrzeć najpierw tutaj. Jeśli zaś masz już to za sobą, to życzę miłej lektury.
Podobnie jak w przypadku jednocząsteczkowej reakcji chemicznej, rozpad jądra jest reakcją pierwszego rzędu. Przypomnijmy sobie zatem odpowiedni wzór na równanie kinetyczne:
![Rendered by QuickLaTeX.com $$ v=k[A] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a786780286138949aead6b45422cbfc6_l3.png)
Jak wiadomo,  to chwilowa szybkość reakcji,
to chwilowa szybkość reakcji, 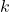 – stała szybkości reakcji, a
– stała szybkości reakcji, a ![Rendered by QuickLaTeX.com [A]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-883cb9ba1f5e71563ce57fee223b9a2a_l3.png) – chwilowe stężenie substratu
– chwilowe stężenie substratu 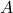 . Przy opisie rozpadów promieniotwórczych zamiast szybkości reakcji posługujemy się pojęciem aktywności, którą określa się jako liczbę rozpadów jądrowych w danym przedziale czasu podzieloną przez długość tego przedziału. Jednostek aktywności jest wiele, choć najczęściej używa się bekerela (
. Przy opisie rozpadów promieniotwórczych zamiast szybkości reakcji posługujemy się pojęciem aktywności, którą określa się jako liczbę rozpadów jądrowych w danym przedziale czasu podzieloną przez długość tego przedziału. Jednostek aktywności jest wiele, choć najczęściej używa się bekerela ( ), czyli
), czyli 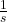 (rozpad na sekundę). W związku z tym, zamiast stężenia reagenta używamy
(rozpad na sekundę). W związku z tym, zamiast stężenia reagenta używamy 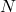 , czyli liczby obecnych w układzie jąder promieniotwórczego „substratu”. W związku z powyższym, analogiem równania kinetycznego dla rozpadów jądrowych jest:
, czyli liczby obecnych w układzie jąder promieniotwórczego „substratu”. W związku z powyższym, analogiem równania kinetycznego dla rozpadów jądrowych jest:
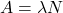
Lambda 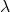 to po prostu alternatywne oznaczenie stałej szybkości, która w tym kontekście jest nazywana stałą rozpadu. Powyższa zależność jest czasem nazywana prawem rozpadu promieniotwórczego.
to po prostu alternatywne oznaczenie stałej szybkości, która w tym kontekście jest nazywana stałą rozpadu. Powyższa zależność jest czasem nazywana prawem rozpadu promieniotwórczego.
Analogicznie możemy z odpowiedniego wzoru dla reakcji pierwszego rzędu wyprowadzić sobie zależność określającą liczbę 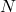 jąder „substratu” po czasie
jąder „substratu” po czasie 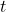 .
.
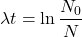
Inaczej:
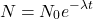
gdzie 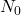 to początkowa liczba jąder promieniotwórczego „substratu”. Wobec tego okres półtrwania, czyli czas, w którym
to początkowa liczba jąder promieniotwórczego „substratu”. Wobec tego okres półtrwania, czyli czas, w którym 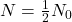 , można powiązać z
, można powiązać z 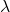 równaniem:
równaniem:
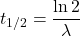
Jądra o dłuższym okresie półtrwania są mniej podatne na rozpad niż te o krótszym. Pamiętajmy jednak, że rozpad promieniotwórczy jest przypadkowy. Pomimo że możemy wyznaczyć aktywność danej próbki, nie jesteśmy w stanie określić, które konkretnie jądro rozpadnie się w wybranym przedziale czasu. Ponadto, prawdopodobieństwo takiego rozpadu w ciągu, powiedzmy, jednej sekundy jest bardzo małe. Na przykład próbka 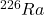 o aktywności
o aktywności 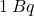 zawiera około
zawiera około 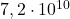 atomów tego izotopu. Oznacza to, że w ciągu jednej sekundy rozpadnie się średnio tylko jedno z tych jąder.
atomów tego izotopu. Oznacza to, że w ciągu jednej sekundy rozpadnie się średnio tylko jedno z tych jąder.
Zadanko – Problem 11 – 39 IChO, Moskwa – Preparatory Problems
Oryginał: https://www.icho.sk/files/documents/preparatory-problems/series-2/preparatory%20problems%20icho%202007.pdf (strona 50)
Radioaktywny izotop węgla, węgiel-14, jest często wykorzystywany w archeologii, geologii i hydrogeologii do datowania próbek. Czas połowicznego rozpadu węgla-14 wynosi 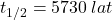 , ale przy obliczaniu wieku próbek stosowana jest inna wartość,
, ale przy obliczaniu wieku próbek stosowana jest inna wartość, 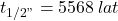 .
. 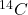 powstaje w atmosferze z azotu, pod wpływem promieniowania kosmicznego. Następnie, w wyniku fotosyntezy oraz poprzez łańcuchy pokarmowe, może znaleźć się w organizmach roślin i zwierząt. Zawartość „radiowęgla” (ang. radiocarbon) w żywych organizmach jest niemal stała; aktywność
powstaje w atmosferze z azotu, pod wpływem promieniowania kosmicznego. Następnie, w wyniku fotosyntezy oraz poprzez łańcuchy pokarmowe, może znaleźć się w organizmach roślin i zwierząt. Zawartość „radiowęgla” (ang. radiocarbon) w żywych organizmach jest niemal stała; aktywność 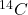 wynosi w nich
wynosi w nich 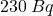 na kilogram węgla. Po śmierci organizmu wymiana węgla z otoczeniem ustaje, więc zawartość
na kilogram węgla. Po śmierci organizmu wymiana węgla z otoczeniem ustaje, więc zawartość 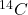 zaczyna systematycznie spadać.
zaczyna systematycznie spadać.
1. Podaj zbilansowane równania reakcji powstawania i rozkładu 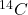 .
.
2. Aktywność „radiowęgla” w próbce tkaniny z egipskiej piramidy odpowiada 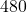 rozpadom na godzinę na gram węgla. Jaki jest wiek tkaniny?
rozpadom na godzinę na gram węgla. Jaki jest wiek tkaniny?
W innej piramidzie znaleziony został pewien biały proszek. Analiza wykazała, że była to czysta fenoksymetylopenicylina (penicylina V):
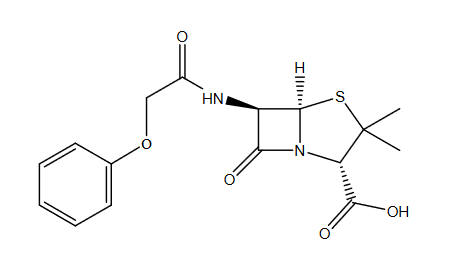
Komercyjna fenoksymetylopenicylina produkowana jest przez mikroorganizmy hodowane na pożywce zawierającej węglowodany (laktozę, glukozę, sacharozę), namok kukurydziany, sole mineralne i kwas fenoksyoctowy.
Aby oszacować wiek proszku, postanowiono zbadać jego zawartość węgla-14. Ustalony za pomocą spektrometrii mas stosunek 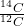 wynosi
wynosi 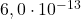 .
.
3. Archeologowie oszacowali wiek proszku, korzystając z prawa rozpadu promieniotwórczego. Na jaką datę produkcji wskazują szacunki?
4. Wyjaśnij ten rezultat. Kiedy w rzeczywistości wyprodukowano proszek?
Wartości stałych według:
Lloyd A. Currie. The Remarkable Metrological History of Radiocarbon Dating. // J. Res. Natl. Inst. Stand. Technol. 109, 185-217 (2004)

Spróbuj najpierw rozwiązać zadanko samodzielnie
Rozwiązanie:
1. Tworzenie: 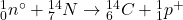
Rozpad: 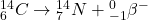
2. Przypomnijmy prawo rozpadu promieniotwórczego i przekształćmy je w odpowiedni sposób. Warto zauważyć, że zamiast 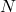 możemy w analogiczne miejsce podstawić
możemy w analogiczne miejsce podstawić 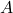 (aktywność),
(aktywność),  (stężenie),
(stężenie), 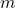 (masę izotopu promieniotwórczego) lub
(masę izotopu promieniotwórczego) lub 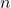 (liczbę moli), gdyż one wszystkie są liniowo (wprost) proporcjonalne:
(liczbę moli), gdyż one wszystkie są liniowo (wprost) proporcjonalne:
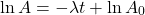
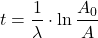
Obliczamy potrzebne dane, pamiętając o jednostkach:
![Rendered by QuickLaTeX.com $$ A &=480\left[\frac{1}{h \cdot g}\right]=\frac{480}{3600}\left[\frac{1}{s \cdot g}\right] \approx 0,1333\left[\frac{1}{s \cdot g}\right] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-04a8bf347de039493e18e6913a095e47_l3.png)
![Rendered by QuickLaTeX.com $$ A_{0} &=230\left[\frac{1}{s \cdot k g}\right]=\frac{230}{1000}\left[\frac{1}{s \cdot g}\right]=0,23\left[\frac{1}{s \cdot g}\right] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e30c42018b2a3e8af966aa81f35a5551_l3.png)
![Rendered by QuickLaTeX.com $$ t_{1/2"}=\frac{\ln 2}{\lambda}=5568[lat] \approx 1,757 \cdot 10^{11}[s] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-89fda5d58aa64deaac6bb8bf80b12775_l3.png)
![Rendered by QuickLaTeX.com $$ \lambda &=3,94506 \cdot 10^{-12}\left[s^{-1}\right] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0d55d273b7fa37458e3ec2b1a127c5bb_l3.png)
Po podstawieniu otrzymujemy:
![Rendered by QuickLaTeX.com $$ t \approx 1,383 \cdot 10^{11}[s] \approx 4381,46[lat] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-41b467098fdd8870036ebbb0b35300c1_l3.png)
3. W obiegu biologicznym ![Rendered by QuickLaTeX.com A_{0}=0,23\left[\frac{B q}{g}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-033ad5e5f1181596dfc8fa22282bd12e_l3.png) (bekereli na gram węgla)
(bekereli na gram węgla)
Obliczmy zatem zawartość początkową 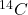 oraz
oraz 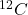 w gramie węgla.
w gramie węgla. 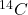 jest jedynym izotopem promieniotwórczym w tej próbce, toteż jego aktywność równa się aktywności próbki:
jest jedynym izotopem promieniotwórczym w tej próbce, toteż jego aktywność równa się aktywności próbki:
![Rendered by QuickLaTeX.com N_{C-14}=\frac{A_{0}}{\lambda}=\frac{0,23\left[\frac{1}{s \cdot g}\right]}{3,945 \cdot 10^{-12}\left[\frac{1}{s}\right]}=5,83 \cdot 10^{10}\left[\frac{1}{g}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-07342f9b1571b6b460e36c87f1d65013_l3.png)
Można przyjąć, że ilość 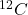 jest w tak dużym nadmiarze, że jest ona stała oraz składa się z niego cała próbka:
jest w tak dużym nadmiarze, że jest ona stała oraz składa się z niego cała próbka:
![Rendered by QuickLaTeX.com N_{C-12}=\frac{m}{M_{C-12}} \cdot N_{A}=\frac{1}{12}\left[\frac{\mathrm{mol}}{\mathrm{g}}\right] \cdot 6,022 \cdot 10^{23}\left[\frac{1}{\mathrm{mol}}\right] \approx 5,02 \cdot 10^{22}\left[\frac{1}{\mathrm{g}}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4601b0ab657a8a321b57a3e10ce42ca2_l3.png)
Posiadając te dane, porównajmy początkową proporcję 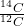 z tą wyznaczoną dla badanego proszku:
z tą wyznaczoną dla badanego proszku:
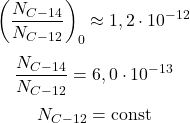
Rozpadła się połowa węgla 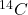 , czyli:
, czyli:
![Rendered by QuickLaTeX.com $$ t=t_{1/ 2}=5568[lat] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a8ff160d4bfe126fbfa0875b57951a83_l3.png)
4. Pomyślmy nad tym, skąd wzięły się substraty do syntezy tej tworzonej przez mikroorganizmy penicyliny. Można założyć, że cukry oraz syrop kukurydziany były z obiegu biologicznego, a sole mineralne najpewniej nie zostały wbudowane w jej strukturę. Kwas fenoksyoctowy zaś otrzymuje się (wieloetapowo) z paliw kopalnych, które mają praktycznie zerową zawartość 14C, gdyż mają miliony lat. Należy zauważyć, że z tego kwasu pochodzi osiem z szesnastu, czyli 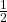 atomów węgla w każdej cząsteczce penicyliny V. Aby skorzystać poprawnie z wyników datowania węglowego, wszystkie atomy węgla w cząsteczce muszą pochodzić z obiegu biologicznego. W naszym przypadku możemy udać, że tak jest, mnożąc wyznaczony doświadczalnie stosunek ilość poszczególnych izotopów węgla przez dwa. Otrzymujemy wtedy:
atomów węgla w każdej cząsteczce penicyliny V. Aby skorzystać poprawnie z wyników datowania węglowego, wszystkie atomy węgla w cząsteczce muszą pochodzić z obiegu biologicznego. W naszym przypadku możemy udać, że tak jest, mnożąc wyznaczony doświadczalnie stosunek ilość poszczególnych izotopów węgla przez dwa. Otrzymujemy wtedy:
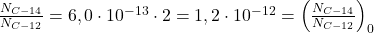
czyli ![Rendered by QuickLaTeX.com t \sim 0[s]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-75a24c6cb9f0d8563dd1a65f1e7914d7_l3.png) . Czemu „
. Czemu „ ” zamiast „
” zamiast „ „? Pamiętajmy, że każdy pomiar obarczony jest niepewnością. Otrzymany wynik świadczy zatem, że penicylina pochodzi z ostatnich kilkudziesięciu lat.
„? Pamiętajmy, że każdy pomiar obarczony jest niepewnością. Otrzymany wynik świadczy zatem, że penicylina pochodzi z ostatnich kilkudziesięciu lat.
Rozpady promieniotwórcze jako reakcje następcze
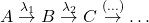
Kiedy powstające w rozpadzie promieniotwórczym jądro również jest promieniotwórcze i wykazuje pewną aktywność, mamy do czynienia z następczym rozpadem promieniotwórczym. Jeśli również kolejne powstające jądra są promieniotwórcze, powstaje szereg (łańcuch) promieniotwórczy, którego końcem jest stabilny izotop nieulegający dalszym rozpadom. W przyrodzie występują trzy takie szeregi: uranowo-radowy, uranowo-aktynowy oraz torowy.
Pomiędzy każdą parą „sąsiadujących w szeregu” nuklidów występują związki określone przez stałe rozpadu danych nuklidów – dokładnie tak samo, jak w klasycznych reakcjach następczych. Dla rozpadów promieniotwórczych zależności te nazywane są równaniami Batemana i przedstawiają się następująco. Wyprowadzenie wzorów znajdziecie we wpisie o reakcjach następczych.
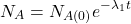
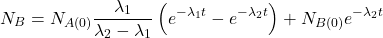
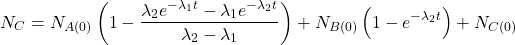
W większości przypadków przyjmujemy założenie, że dla 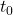 w układzie występuje tylko nuklid
w układzie występuje tylko nuklid 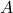 , czyli
, czyli 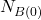 i
i 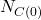 wynoszą 0, więc równania możemy uprościć do:
wynoszą 0, więc równania możemy uprościć do:
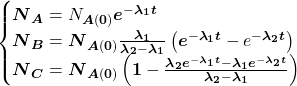
Zadanko – Zadanie 4. „Mineralne składniki piasku z plaży w Kerala” – 33. IChO, Bombaj
Oryginał: https://www.icho.sk/files/documents/competition-problems/volume%202%20-%20icho%2021-40.pdf (strona 386) [Poniższe tłumaczenie pochodzi ze strony Olchemu]
Zawarty w piasku plaży minerał monazyt jest bogatym źródłem toru, dostępnym w dużych ilościach w indyjskim stanie Kerala. Typowa próbka monazytu zawiera około 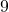 i
i 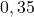 . Izotopy
. Izotopy 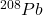 i
i 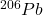 są trwałymi końcowymi produktami w szeregach rozpadu promieniotwórczego – odpowiednio –
są trwałymi końcowymi produktami w szeregach rozpadu promieniotwórczego – odpowiednio – 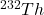 i
i 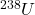 . Cała ilość ołowiu (
. Cała ilość ołowiu (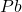 ) znajdywana w monazycie jest pochodzenia radiogenicznego.
) znajdywana w monazycie jest pochodzenia radiogenicznego.
Stosunek zawartości atomów – izotopów 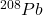 /
/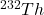 w próbce monazytu, zmierzony metodą spektrometrii masowej, wynosił
w próbce monazytu, zmierzony metodą spektrometrii masowej, wynosił 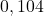 . Okresy połowicznego rozpadu
. Okresy połowicznego rozpadu 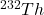 oraz
oraz 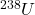 wynoszą, odpowiednio,
wynoszą, odpowiednio, 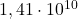 lat i
lat i 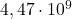 lat. Załóż, że cała ilość
lat. Załóż, że cała ilość 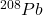 ,
, 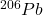 ,
, 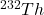 oraz
oraz 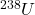 pozostała w próbce monazytu od czasu powstania tego minerału.
pozostała w próbce monazytu od czasu powstania tego minerału.
4.1 Oblicz wiek próbki monazytu (czas, który upłynął od momentu jego utworzenia).
4.2 Oszacuj stosunek zawartości izotopów 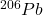 /
/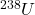 w próbce monazytu.
w próbce monazytu.
4.3 Tor-232 jest materiałem paliworodnym w energetyce nuklearnej. W trakcie napromieniania neutronami termicznymi, izotop ten absorbuje neutron a powstający izotop tworzy 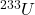 przez kolejne rozpady
przez kolejne rozpady 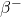 . Zapisz równania reakcji jądrowych dla tworzenia
. Zapisz równania reakcji jądrowych dla tworzenia 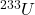 z
z 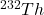 .
.
W czasie jądrowego rozszczepienia 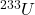 powstaje złożona mieszanina radioaktywnych produktów takiego rozszczepienia. Produkt rozszczepienia
powstaje złożona mieszanina radioaktywnych produktów takiego rozszczepienia. Produkt rozszczepienia 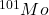 ulega rozpadowi radioaktywnemu zgodnie z poniższym schematem.
ulega rozpadowi radioaktywnemu zgodnie z poniższym schematem.
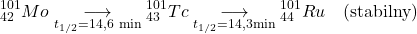
4.4 Świeżo przygotowana, radiochemicznie czysta próbka 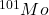 zawiera początkowo
zawiera początkowo 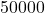 atomów
atomów 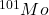 . Ile atomów: (i)
. Ile atomów: (i) 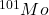 , (ii)
, (ii)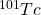 , (iii)
, (iii) 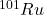 , będzie obecne w próbce po czasie
, będzie obecne w próbce po czasie 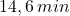 ?
?

Spróbuj najpierw rozwiązać zadanko samodzielnie
Rozwiązanie:
4.1 Tu wystarczy po prostu skorzystać z prawa rozpadu promieniotwórczego. Przedtem należy jednak wyznaczyć początkową liczbę atomów 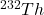 :
:
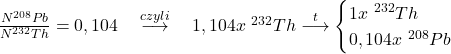
…oraz wartość stałej rozpadu:
![Rendered by QuickLaTeX.com t_{1 / 2}=1,41 \cdot 10^{10}[\text{lat}] \quad \stackrel{czyli}{\longrightarrow} \quad \lambda=\frac{\ln 2}{t_{1 / 2}}=4,92 \cdot 10^{-11}\left[\frac{1}{\text{rok}}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-cd35b4ebf69a49bef49d913a10bd95bc_l3.png)
Podstawiamy wyznaczone dane do równania:
![Rendered by QuickLaTeX.com \boldsymbol{t}=\frac{1}{\lambda} \ln \frac{N_{{ }^{232}{Th}(0)}}{N_{{ }^{232}{Th}}}=\frac{1}{4,92 \cdot 10^{-11}} \ln \frac{1,104}{1}=\mathbf{2}, \mathbf{011} \cdot \mathbf{10}^{\mathbf{9}}[\boldsymbol{lat}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4f0e81ea29db737838514824a30aeca8_l3.png)
4.2 Stosując rozumowanie podobne do tego z poprzedniego podpunktu, tak samo skorzystamy z prawa rozpadu promieniotwórczego. Najpierw wyznaczymy stałą rozpadu:
![Rendered by QuickLaTeX.com t_{1 / 2}=4,47 \cdot 10^{9}[lat] \quad \stackrel{czyli}{\longrightarrow} \quad \lambda=\frac{\ln 2}{t_{1 / 2}}=1,55 \cdot 10^{-10}\left[\frac{1}{\text{rok}}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7ba67f02ce7b1aef59d92d3356f108ca_l3.png)
Podstawiamy do równania:
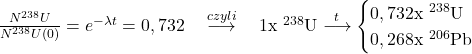
Czyli stosunek zawartości izotopów wynosi:
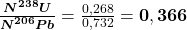
4.3 Równania rozpadów:
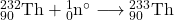
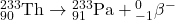
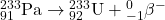
4.4 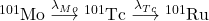
Tu skorzystamy po prostu z równania Batemana (tego dla 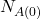 ). Standardowo, potrzebujemy najpierw wyznaczyć obie stałe rozpadu:
). Standardowo, potrzebujemy najpierw wyznaczyć obie stałe rozpadu:
![Rendered by QuickLaTeX.com t_{1 / 2(\mathrm{Mo})}=14,6[\min ] \quad \stackrel{c z y l i}{\longrightarrow} \quad \lambda_{\mathrm{Mo}}=\frac{\ln 2}{t_{1 / 2}}=0,04748\left[\frac{1}{\min }\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0989e1cf205ed8abe211a4c421b94822_l3.png)
![Rendered by QuickLaTeX.com t_{1 / 2(\mathrm{Tc})}=14,3[\min ] \quad \stackrel{c z y l i}{\longrightarrow} \quad \lambda_{\mathrm{Tc}}=\frac{\ln 2}{t_{1 / 2}}=0,04847\left[\frac{1}{\min }\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ca0bcc73403e19342dc05ad0fe0d32c8_l3.png)
Tak więc liczba jąder poszczególnych izotopów wynosi:
![Rendered by QuickLaTeX.com \boldsymbol{N}_{\boldsymbol{Mo}}=\frac{50000}{2}=\mathbf{25000}[\boldsymbol{atomów}] \quad \leftarrow \text{gdyż} \ t=14,6[\mathrm{min}]=t_{1 / 2}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-cd2728df43f4931b489d73fbb2d6b514_l3.png)
![Rendered by QuickLaTeX.com \boldsymbol{N}_{\boldsymbol{Tc}}=\frac{\lambda_{Mo}}{\lambda_{Tc}-\lambda_{Mo}} \cdot N_{M o(0)} \cdot\left(e^{-\lambda_{Mo} t}-e^{-\lambda_{Tc} t}\right)=\mathbf{17205}[\boldsymbol{atomów}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-9b93bf8ce6fd39def538d5ac89d507ef_l3.png)
![Rendered by QuickLaTeX.com \boldsymbol{N}_{\boldsymbol{Ru}}=50000-25000-17205=\mathbf{7795}[\boldsymbol{atomów}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-591f2fff0cc67799d51289372adcc5e1_l3.png)
Inne zadanka, jakie możecie przerobić:
- Zad. 4 – I etap – 57. Olchem (Dosyć łatwe)
- Zad. B4 – Folder Wstępny – 68. Olchem (Tu wykorzystuje się takie zmodyfikowane równanie Batemana – zamiast
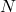 jest
jest 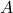 (aktywność), dlatego np. jest zamieniona kolejność stałych. Warto sobie wyprowadzić jedną postać z drugiej (oczywiście dzięki zależności
(aktywność), dlatego np. jest zamieniona kolejność stałych. Warto sobie wyprowadzić jedną postać z drugiej (oczywiście dzięki zależności 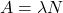 ).
).
Do zobaczenia przy kolejnym wpisie! A, i pamiętajcie o pouczeniu się do olimpiady, bo to już czas.