Wprowadzenie do kinetyki chemicznej
Wprowadzenie do kinetyki chemicznej
W celu uzyskania informacji kinetycznych dotyczących reakcji substytucji nukleofilowej 2-metylo-2-bromopropanu i deuterowanej wody wykonano serie pomiarów. Doświadczenie polegało na wykonaniu miareczkowania argentometrycznego wydzielanego w trakcie reakcji DBr przy użyciu mianowanego roztworu azotanu(V) srebra(I) w różnych odstępach czasu. Reakcję substytucji nukleofilowej związku organicznego prowadzono w D2O o czystości 99,8% z dodatkiem trietyloaminy (TEA). Miało to na celu zapewnić odpowiednie warunki umożliwiające zachodzenie substytucji typu SN1. Objętości titranta zużytego w trakcie miareczkowania zestawiono w poniższej tabeli.
Uwaga: Podczas prowadzenia doświadczenia układ, w którym zachodziła reakcja SN1 był ściśle termostatowany.

*Wartość czasu podana w tej kolumnie jest równoznaczna z czasem po którym reakcja przestała biec.
Polecenia:
a. Napisz stechiometryczne równanie reakcji zachodzącej podczas reakcji SN1.
b. Określ rząd kinetyczny reakcji SN1.
c. Oblicz stałe szybkości reakcji SN1 k1-k6 oraz wartość uśrednioną kśr (zdefiniowaną jako średnia arytmetyczna wszystkich pomiarów). Określ wartość najbardziej odchyloną od wartości średniej. Wyniki stałych szybkości podaj z odpowiednią jednostką zgodną ze standardem SI.
d. Zaproponuj mechanizm omawianej reakcji substytucji. Który etap podanego mechanizmu definiuje szybkość reakcji?
e. Po jakim czasie reakcja przestała biec? Załóż, że koniec reakcji zachodzi wtedy kiedy zużyto 46,27cm3 titranta.
f. Oblicz okres półtrwania reakcji, tj. czas po którym 50% substratu ulegnie przemianie.
Wprowadzenie do kinetyki chemicznej – odpowiedzi do zadania
a. Reakcja SN1 jest przykładem reakcji substytucji nukleofilowej, którą można przedstawić następującym równaniem stechiometrycznym
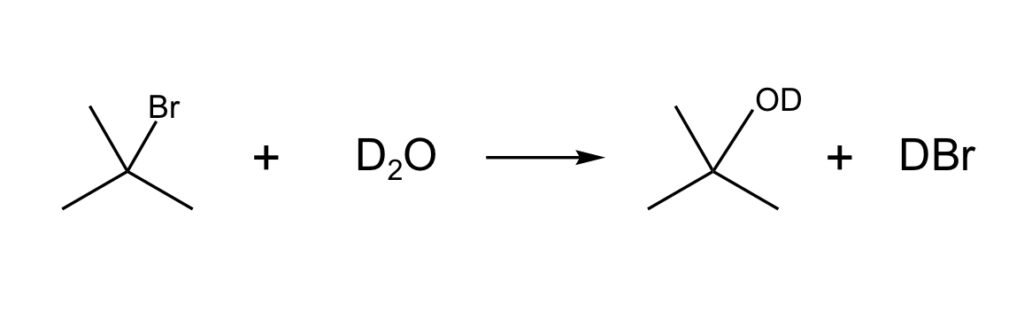
b. Skrót SN1 pochodzi od zwrotu umimolecular nucleophilic substitution reaction. Słowo unimolecular oznacza, że reakcja, która determinuje szybkość całego procesu jest jednocząsteczkową reakcją elementarną. Wiedząc to, można od razu, bez przeprowadzania żadnych obliczeń stwierdzić, że rząd tej reakcji jest równy 1.
c. Wiedząc, że mamy do czynienia z reakcją pierwszego rzędu możemy przywołać scałkowane równanie kinetyczne dla owej reakcji
C(substrat)t=C(substrat)0e-kt
Jednak wiadomo również, że podczas miareczkowania mierzone jest stężenie produktu w danym punkcie w czasie. Zatem można nieco przekształcić podwyższy wzór, tak aby miał zastosowanie do rozwiązania zadania
C(produkt)t=C(produkt)0ekt
Pozbywając się wykładnika i dzieląc przez zmienną niezależną (czas, t) uzyskujemy wyrażenie na stałą szybkości
k=t-1ln(Ct/C0)
Można też zauważyć, że nie mamy podanych bezpośrednio wartości stężenia produktu. Jednakże, nie stanowi to problemu ponieważ po prawej stronie powyższego równania interesuje nas wartość, która zmienia się tak samo jak stężenie. Tą wartością jest objętość titranta. Dodatkowo, jeżeli mamy do policzenia stosunek tych wartości to jednostka nie gra roli ponieważ się skraca. Stąd
k=t-1ln(Vt/V0)
Gdzie V to objętości titranta zużyte w danych punktach w czasie miareczkowania. Vt symbolizuje wartość objętości jaka została zużyta po danym czasie, a V0 objętość jaka została zużyta na początku dokonywania pomiaru. Równanie to w sposób prosty można zaaplikować do rozwiązania problemu podstawiając konkretne wartości podane w tabelce. Należy też zwrócić uwagę, że podstawianie wartości t w tym wzorze oznacza zmianę czasu jaka nastąpiła od pierwszego pomiaru do drugiego. Czas ten wygodnie jest przekształcić na jednostki podane w sekundach- jednostki zgodne z układem SI.
k1=600-1ln(14,70/11,19)=4,547·10-4 s-1
k2=1200-1ln(19,32/11,19)=4,551·10-4s-1
k3=1800-1ln(25,38/11,19)=4,550·10-4s-1
k4=2400-1ln(33,35/11,19)=4,550·10-4s-1
k5=600-1ln(25,38/19,32)=4,547·10-4 s-1
k6=1200-1ln(25,38/14,70)=4,551·10-4s-1
kśr= 4,549·10-4s-1
Wartości najbardziej odchylone od wartości średniej pogrubiono. Jest także istotne, aby nadmienić że dokładność z jaką należy podać wyniki stałej szybkości powinny być podane do 4. miejsca znaczącego- z taką dokładnością została zarejestrowana mierzona wartość (objętość zużytego titranta).
d. Szybkość sumarycznej reakcji determinuje szybkość tej reakcji elementarnej, która zachodzi najwolniej. Poniżej przedstawiono mechanizm omawianej przemiany.
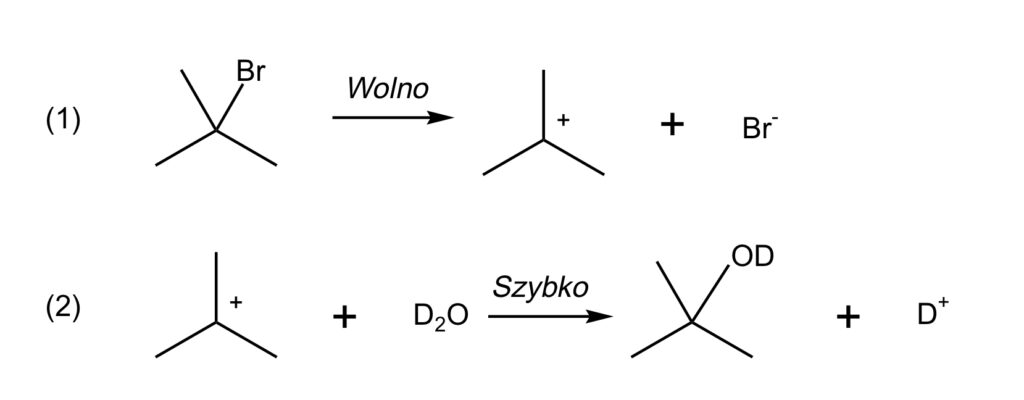
Etap (1) zatem determinuje szybkość badanej reakcji.
e. Po pomyślnym obliczeniu wartości stałej szybkości, obliczenie czasu, po którym reakcja przestała biec nie stanowi problemu. Należy przekształcić wzór „na t” i podstawić znane wartości. Stąd
t=k-1ln(Vt/V0)= (4,549·10-4)-1ln(46,27/33,35)=719,8s≈12min
Więc, reakcja przestała biec po 50+12=62min.
f. Okres półtrwania, τ, oznacza czas, po którym połowa ilości początkowej substratu ulega reakcji. Dla reakcji pierwszego rzędu jest to dość prosta zależność
τ=k-1ln2=(4,549·10-4)-1ln2=1524s