Wskazówki do zadań z chemii analitycznej dla początkujących + Dać chemikowi kawałek metalu… – rozwiązanie
Uwaga, ten post jest dość długi. Zalecane przygotowanie sobie herbatki tudzież innego napoju, wedle preferencji.
W wyniku pewnych turbulencji, dopiero teraz publikujemy rozwiązanie zadania sprzed trzech miesięcy.
Z treścią zadania można zapoznać się tutaj. Sugeruję to nawet osobom, które już wcześniej to zrobiły, gdyż w wyniku błędu (czy też karygodnego niedomówienia) w danych literaturowych, treść musiała zostać dość mocno zmodyfikowana.

Żeby jednak za to wszystko zadośćuczynić, rozwiązanie jest dość szczegółowe. Przy tym poprzetykane wskazówkami, które mogą dla wielu wydawać się oczywiste, ale jeżeli dopiero rozpoczynasz swoją przygodę z chemią czy z Olimpiadą Chemiczną albo uczysz się samodzielnie, są one nieocenione. Dotyczą one raczej strony technicznej rozwiązywania takich problemów – mniej lub bardziej oficjalnych konwencji czy sposobów na oszczędzenie czasu.
a) Oblicz procent masowy cynku.
Z zimnym kwasem siarkowym reaguje cynk (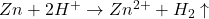 ), natomiast miedź, jako metal nieroztwarzający się w kwasach nieutleniających (inaczej: metal mniej aktywny od wodoru; inaczej: metal o wyraźnie wyższym od wodoru standardowym potencjale redukcyjnym etc.) reagować nie będzie. Informacja o „bardzo dokładnym rozdrobnieniu” ma sugerować, że cynk roztworzył się ilościowo, natomiast brak dodatkowych informacji powoduje, że gaz musimy uznać za doskonały:
), natomiast miedź, jako metal nieroztwarzający się w kwasach nieutleniających (inaczej: metal mniej aktywny od wodoru; inaczej: metal o wyraźnie wyższym od wodoru standardowym potencjale redukcyjnym etc.) reagować nie będzie. Informacja o „bardzo dokładnym rozdrobnieniu” ma sugerować, że cynk roztworzył się ilościowo, natomiast brak dodatkowych informacji powoduje, że gaz musimy uznać za doskonały:
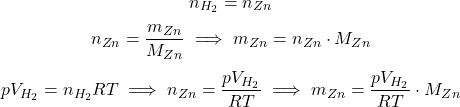
Należy jeszcze zwrócić uwagę na jednostki – został zastosowany tani chwyt – wartość ciśnienia odpowiada liczbowo ciśnieniu normalnemu, do którego jesteśmy przyzwyczajeni, natomiast jego jednostką są tory, a nie (hekto)paskale:
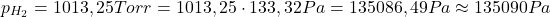
Wobec tego:
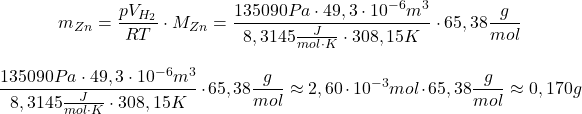
Wskazówka. Jednostki przy obliczeniach w zdecydowanej większości przypadków są „tylko dla Ciebie”. Na Olimpiadzie za ich brak raczej nie biją, tutaj także będą one wypisywane tylko wtedy, kiedy nie są oczywiste. Dobrym nawykiem przy wyprowadzaniu wzorów jest przeprowadzanie analizy wymiarowej, czyli rozbicie jednostek na „bardziej podstawowe”, poskracanie ich i sprawdzenie, czy jednostka, w jakiej podawany jest wynik, jest poprawna. Często szkoda na to czasu – na pewno jednak zawsze warto pozbywać się przedrostków (tzn. zamieniać np. 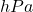 na
na 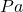 ), gdyż zmniejsza to szanse na popełnienie błędu rachunkowego.
), gdyż zmniejsza to szanse na popełnienie błędu rachunkowego.
Pozostaje tylko obliczyć procent masowy, z podaną w poleceniu dokładnością:
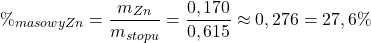
b) Oblicz pH roztworu, czy strącą się osady wodorotlenków?
We wszystkich poniższych obliczeniach uznajemy autodysocjację wody za zjawisko pomijalne i jej nie uwzględniamy. Aby obliczyć 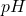 roztworu, należy najpierw wyznaczyć stężenie analityczne (tj. stężenie wszystkich form protonacyjnych) cyjanku:
roztworu, należy najpierw wyznaczyć stężenie analityczne (tj. stężenie wszystkich form protonacyjnych) cyjanku:
![Rendered by QuickLaTeX.com $$ [HCN] + [ CN^{-} ] = c_{CN^{-}} = \frac{n_{CN^{-}}}{V} = \frac{m_{KCN}}{M_{KCN}} \cdot \frac{1}{V} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-1fc4ac9428c343e5dccc6cba0e1cc0ed_l3.png)
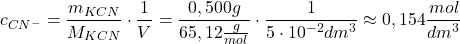
Teraz należy zastanowić się, jak na 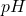 roztworu wpłynie dodanie
roztworu wpłynie dodanie 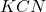 . Jest to sól mocnej zasady i słabego kwasu – kwasu o
. Jest to sól mocnej zasady i słabego kwasu – kwasu o 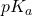 zdecydowanie mniejszym od 7. Znaczy to tyle, że dodanie jej do wody (o odczynie obojętnym) spowoduje protonowanie jonów cyjankowych i zwiększenie się
zdecydowanie mniejszym od 7. Znaczy to tyle, że dodanie jej do wody (o odczynie obojętnym) spowoduje protonowanie jonów cyjankowych i zwiększenie się 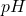 . Innymi słowy, reakcja
. Innymi słowy, reakcja
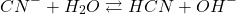
przebiega w prawo, aż do ustalenia się równowagi.
Wskazówka. Zauważ, że dla tej reakcji (i każdej tego typu reakcji równowagowej między sprzężonymi kwasem i zasadą Brønsteda) stężenia 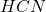 i
i 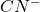 są sobie równe, gdy
są sobie równe, gdy 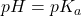 . Gdy
. Gdy 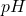 maleje poniżej wartości
maleje poniżej wartości 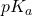 , zwiększa się udział formy sprotonowanej, a gdy rośnie, zwiększa się udział formy zdeprotonowanej. Spróbuj wyprowadzić to samodzielnie, przy użyciu równania na stałą równowagi takiej reakcji oraz równania na stałą dysocjacji (i pamiętaj, że
, zwiększa się udział formy sprotonowanej, a gdy rośnie, zwiększa się udział formy zdeprotonowanej. Spróbuj wyprowadzić to samodzielnie, przy użyciu równania na stałą równowagi takiej reakcji oraz równania na stałą dysocjacji (i pamiętaj, że ![Rendered by QuickLaTeX.com [OH^{-}] = \frac{K_{w}}{[H^{+}] }](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-bcb47190375291e9765aaf27eb7ed63f_l3.png) ).
).
Tak czy inaczej, wiemy, że 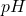 będzie się zmieniać w wyniku reakcji opisanej powyżej. Ponieważ pomijamy autodysocjację wody (czyli zakładamy, że przed dodaniem
będzie się zmieniać w wyniku reakcji opisanej powyżej. Ponieważ pomijamy autodysocjację wody (czyli zakładamy, że przed dodaniem ![Rendered by QuickLaTeX.com KCN\:[ OH^{-} ] \approx 0](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-88f13ad5b32c28c5277c4eb61a0ca000_l3.png) ), bezpośrednio z równania reakcji możemy wywnioskować, że:
), bezpośrednio z równania reakcji możemy wywnioskować, że:
![Rendered by QuickLaTeX.com $$ [HCN] = [OH^{-}] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-edef5fc33fa4aeb5090b766111fcb49b_l3.png)
Z definicji stężenia analitycznego wiemy, że:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [HCN] + [ CN^{-} ] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-76088009d5b701759477c27bc5b07ba3_l3.png)
Wobec tego możemy już obliczyć stężenie jonów wodorowych w roztworze. Wychodząc z wyrażenia na stałą dysocjacji 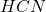 :
:
![Rendered by QuickLaTeX.com $$ K_{a} = \frac{ [CN^{-}] [H^{+}] }{ [HCN] }$$ $$ K_{a} = \frac{ (c_{CN^{-}} - [HCN]) \cdot [H^{+}] }{ [HCN] }$$ $$ K_{a} = \frac{ [H^{+}] c_{CN^{-}} }{ [HCN] } - [ H^{+} ]$$ $$ K_{a} = \frac{ [H^{+}] c_{CN^{-}} }{ [OH^{-}] } - [ H^{+} ]$$ $$ K_{a} = [H^{+}] c_{CN^{-}}\frac{ [ H^{+} ] }{K_{w}} - [ H^{+} ]$$ $$ \frac{ c_{CN^{-}} }{K_{w}} [H^{+}]^{2} - [ H^{+} ] - K_{a} = 0 $$ $$ \frac{ 0,154 }{10^{-14}} \cdot [H^{+}]^{2} - [ H^{+} ] - 10^{-9,36} = 0 $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e9c78ad1deede06a67d913b21403b92c_l3.png)
Takie równanie kwadratowe jest już do rozwiązania, jako jedyny sensowny wynik otrzymujemy ![Rendered by QuickLaTeX.com [H^{+}] \approx 5,36\cdot10^{-12}\:(\frac{mol}{dm^{3}})](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7fbfc43f4aeed3e53e34eeae221602e5_l3.png) . W takim wypadku
. W takim wypadku 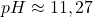 , natomiast
, natomiast ![Rendered by QuickLaTeX.com [OH^{-}] \approx 1,87\cdot10^{-3}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-8accb9f0491dffac9d048112d465fdf1_l3.png) .
.
Wskazówka. Wyrażenie „stężenie jonów wodorowych” i zapis ![Rendered by QuickLaTeX.com [H^{+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4af52cb7d3bf6d7c2d14d9c8b298c20f_l3.png) są w pewien sposób niepoprawne, gdyż w roztworze nie mogą istnieć „gołe” jony wodorowe
są w pewien sposób niepoprawne, gdyż w roztworze nie mogą istnieć „gołe” jony wodorowe 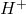 (które de facto są po prostu protonami). Są one zawsze solwatowane przez cząsteczki rozpuszczalnika, zatem poprawniej rzeczywistość opisuje wyrażenie
(które de facto są po prostu protonami). Są one zawsze solwatowane przez cząsteczki rozpuszczalnika, zatem poprawniej rzeczywistość opisuje wyrażenie 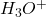 , a „jeszcze poprawniej”
, a „jeszcze poprawniej” 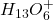 . Jednak zapis
. Jednak zapis 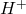 , zarówno w chemii analitycznej, jak i przy równaniach redox, jest uznawany za akceptowalne uproszczenie. Podobnie,
, zarówno w chemii analitycznej, jak i przy równaniach redox, jest uznawany za akceptowalne uproszczenie. Podobnie, 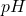 nie jest miarą stężenia „jonów wodorowych”, ale raczej ich aktywności – wprowadzenie pojęcia aktywności wymagałoby jednak osobnego postu. Dość powiedzieć, że w warunkach temperatur bliskich pokojowej i przy niezbyt wysokich stężeniach aktywność jest niemalże równa stężeniu i to również jest uznawane za akceptowalne przybliżenie.
nie jest miarą stężenia „jonów wodorowych”, ale raczej ich aktywności – wprowadzenie pojęcia aktywności wymagałoby jednak osobnego postu. Dość powiedzieć, że w warunkach temperatur bliskich pokojowej i przy niezbyt wysokich stężeniach aktywność jest niemalże równa stężeniu i to również jest uznawane za akceptowalne przybliżenie.
Teraz pora sprawdzić, czy z naszego roztworu przy takim 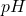 strąciłyby się jakieś wodorotlenki. Wiemy, że wyrażenie na
strąciłyby się jakieś wodorotlenki. Wiemy, że wyrażenie na 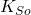 związku typu
związku typu 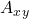 ma postać
ma postać ![Rendered by QuickLaTeX.com [A]^{x}[B]^{y}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7b6080631e472e759ef345066e100fa2_l3.png) . Stała
. Stała 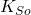 określa maksymalną „dopuszczalną” wartość tego iloczynu, zatem jeżeli jego wartość w danym momencie jest większa od stałej, to związek będzie się wytrącać.
określa maksymalną „dopuszczalną” wartość tego iloczynu, zatem jeżeli jego wartość w danym momencie jest większa od stałej, to związek będzie się wytrącać.
Obliczmy najpierw stężenia molowe jonów 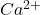 i
i 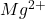 :
:
![Rendered by QuickLaTeX.com $$ [Ca^{2+}] = \frac{0,208 g}{40,08 \frac{g}{mol}} \cdot \frac{1}{1 dm^{3}} \approx 5,19\cdot10^{-3} \frac{mol}{dm^{3}} $$ $$ [Mg^{2+}] = \frac{0,1283 g}{24,31 \frac{g}{mol}} \cdot \frac{1}{1 dm^{3}} \approx 5,28\cdot10^{-3} \frac{mol}{dm^{3}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-82c6aed1712b1d85835aa8e0167d924c_l3.png)
A teraz sprawdźmy wartość wyrażeń na 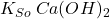 oraz
oraz 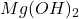 (oczywiście,
(oczywiście, 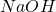 i
i 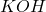 są rozpuszczalne bardzo dobrze, więc nie zawracamy sobie nimi głowy):
są rozpuszczalne bardzo dobrze, więc nie zawracamy sobie nimi głowy):
![Rendered by QuickLaTeX.com $$ [Ca^{2+}][OH^{-}]^{2} = 5,19\cdot10^{-3} \cdot (1,87\cdot10^{-3})^{2} \approx 1,81\cdot10^{-8} $$ $$ [Mg^{2+}][OH^{-}]^{2} = 5,28\cdot10^{-3} \cdot (1,87\cdot10^{-3})^{2} \approx 1,85\cdot10^{-8} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-247706edaa56173fbcf4cf71612e4ac1_l3.png)
I porównanie tego z wartościami 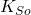 :
:
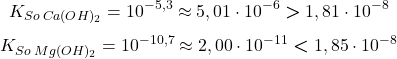
Zatem tak, wytrącą się nieapetyczne osady wodorotlenków – iloczyn stężeń przekracza wartość 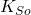 (tylko) w przypadku
(tylko) w przypadku 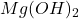 – osad
– osad 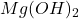 się strąci (można nawet obliczyć, ile go będzie).
się strąci (można nawet obliczyć, ile go będzie).
c) Wyraź cZn w zależności od cCu.
Krótszy i łatwiejszy podpunkt – stężenie całkowite jest wprost proporcjonalne do liczby moli danego indywiduum chemicznego w roztworze:
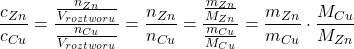
Czyli:
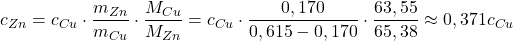
(Mimo że stop ma inną masę niż w podpunkcie a), człon 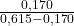 jest prawidłowy, ponieważ korzystamy tu ze stosunku mas cynku i miedzi, a ten jest stały, niezależnie od wielkości próbki. Zamiast tych mas, można by skorzystać z wyznaczonych procentów, ale wiązałoby się to z obniżeniem dokładności).
jest prawidłowy, ponieważ korzystamy tu ze stosunku mas cynku i miedzi, a ten jest stały, niezależnie od wielkości próbki. Zamiast tych mas, można by skorzystać z wyznaczonych procentów, ale wiązałoby się to z obniżeniem dokładności).
Wskazówka. Powyższe obliczenia to tak naprawdę troszeczkę zawoalowane przekształcenie masy na mole – choć, jak za chwilę się okaże, konieczne, to jednak zazwyczaj robione przy okazji rozwiązywania bardziej złożonego problemu. Takie polecenia również się zdarzają na Olchemie, chociaż nieczęsto i raczej na pierwszym etapie – mają na celu zdekoncentrowanie rozwiązującego zadanie, wybicie go z rytmu.
d) Zapisz równanie na stężenie analityczne cyjanków.
Nie ma tu zbyt wiele filozofii, jeśli tylko wiemy, jaki jest sens stężenia analitycznego. Oznacza ono – tak jak ujęto to w poleceniu – sumę stężeń wszystkich form danego indywiduum chemicznego.
Formami, w jakich jon cyjankowy występuje w opisanym układzie, są „wolny” cyjanek 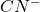 , sprotonowany cyjanek – cyjanowodór
, sprotonowany cyjanek – cyjanowodór 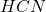 oraz dwa (gdyż założyliśmy, że inne się nie tworzą) kompleksy metali –
oraz dwa (gdyż założyliśmy, że inne się nie tworzą) kompleksy metali – ![Rendered by QuickLaTeX.com [Cu(CN)_{4}]^{3-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-75e388c107a5a8f05b43f16598e5049c_l3.png) oraz
oraz ![Rendered by QuickLaTeX.com [Zn(CN)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13bc8ee19017b0adc3775ee6f42f69ae_l3.png) .
.
Należy jednak zauważyć, że każdą z tych form musimy uwzględnić w odpowiedni sposób. Możemy uznać, że np. jeden mol kompleksu ![Rendered by QuickLaTeX.com [Zn(CN)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13bc8ee19017b0adc3775ee6f42f69ae_l3.png) powstał z jednego mola
powstał z jednego mola 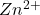 oraz czterech moli
oraz czterech moli 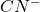 (co w zasadzie jest prawdą, choć nosi znamiona uproszczenia); inaczej: jeden mol
(co w zasadzie jest prawdą, choć nosi znamiona uproszczenia); inaczej: jeden mol ![Rendered by QuickLaTeX.com [Zn(CN)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13bc8ee19017b0adc3775ee6f42f69ae_l3.png) można teoretycznie rozłożyć do czterech moli
można teoretycznie rozłożyć do czterech moli 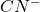 . Stężenie
. Stężenie ![Rendered by QuickLaTeX.com [Zn(CN)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13bc8ee19017b0adc3775ee6f42f69ae_l3.png) przy liczeniu
przy liczeniu 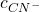 należy zatem policzyć czterokrotnie. Podobnie sprawa ma się z
należy zatem policzyć czterokrotnie. Podobnie sprawa ma się z ![Rendered by QuickLaTeX.com [Cu(CN)_{4}]^{3-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-75e388c107a5a8f05b43f16598e5049c_l3.png) . Odpowiedzią jest więc:
. Odpowiedzią jest więc:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [CN^{-}] + [HCN] + 4[[Cu(CN)_{4}]^{3-}] + 4[[Zn(CN)_{4}]^{2-}] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e5ec31d2b6b19c5edbc43c0f4b191e6d_l3.png)
A teraz chwilka przerwy.

e) Oblicz, ile może co najwyżej ważyć wyjściowa próbka stopu.
Po przerwie nadszedł czas na zdecydowanie najtrudniejszy podpunkt w zadaniu, jego punkt kulminacyjny. Rozwiążemy go najpierw – w celu dydaktycznym – w absolutnie nonsensowny sposób, czyli nie przyjmując uproszczeń innych, niż te podane w treści zadania. Następnie zobaczymy, co dałoby się z tymi obliczeniami zrobić, żeby ułatwić sobie życie.
Najpierw przypomnijmy sobie, jak wygląda wyrażenie na stałą kompleksowania 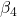 (czyli, w tym wypadku, dla kompleksu metalu z czterema ligandami):
(czyli, w tym wypadku, dla kompleksu metalu z czterema ligandami):
![Rendered by QuickLaTeX.com $$ \beta_{4} = \frac{[ML_{4}]}{[M][L]^{4}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5fbc9102f4c1bb0735310bf6f684bd99_l3.png)
Przy czym ![Rendered by QuickLaTeX.com [M]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ef70acc59d09935de61a763356c5eca1_l3.png) oznacza stężenie „wolnych” jonów metalu (np.
oznacza stężenie „wolnych” jonów metalu (np. 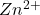 ),
), ![Rendered by QuickLaTeX.com [L]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-79708952fc383a61d3c6dacd3d8ad11f_l3.png) – stężenie „wolnego” liganda (np.
– stężenie „wolnego” liganda (np. 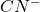 ), natomiast
), natomiast ![Rendered by QuickLaTeX.com [ML_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4545b88f2a1a2ad007e389f64bba3ffd_l3.png) – stężenie kompleksu (w tym przypadku byłoby to stężenie
– stężenie kompleksu (w tym przypadku byłoby to stężenie ![Rendered by QuickLaTeX.com [Zn(CN)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13bc8ee19017b0adc3775ee6f42f69ae_l3.png) ). Należy to rozumieć po prostu jako stałą równowagi reakcji
). Należy to rozumieć po prostu jako stałą równowagi reakcji 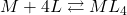 .
.
Wskazówka. Kiedy rozważamy jakiś układ, w którym mamy kilka form wywodzących się z jednego indywiduum chemicznego, obliczenia często są długie i mozolne. Aby trochę zaoszczędzić na czasie, skraca się zapis. Symbole stężeń danych form zwyczajowo upraszcza się – zamiast pisać wzór reszty kwasowej, wstawiamy literę A (od acid), zatem zamiast np. ![Rendered by QuickLaTeX.com [H_{2}C_{2}O_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-6c17b009316e8d72166f9d0834e04102_l3.png) ,
, ![Rendered by QuickLaTeX.com [HC_{2}O_{4}^{-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7fd93ec68a19fd15c3b65933038a3409_l3.png) i
i ![Rendered by QuickLaTeX.com [C_{2}O_{4}^{2-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-73ce18630c25a5a236ba2dba5eddb50a_l3.png) (wiesz, co to za kwas?) mamy po prostu
(wiesz, co to za kwas?) mamy po prostu ![Rendered by QuickLaTeX.com [H_{2}A]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b7e149a6645bc82bd34e4ae9043f0694_l3.png) ,
, ![Rendered by QuickLaTeX.com [HA^{-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0f08a7951c44cbcfa176b029372edcca_l3.png) i
i ![Rendered by QuickLaTeX.com [A^{2-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-816833fa1176a6f25f260548ab1909f8_l3.png) . Podobnie w przypadku kompleksów, zamiast
. Podobnie w przypadku kompleksów, zamiast ![Rendered by QuickLaTeX.com [[Ag(SCN)_{2}]^{-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-287eb4b6dacf5bef2aaf4351ae853019_l3.png) ,
, ![Rendered by QuickLaTeX.com [[Ag(SCN)_{3}]^{2-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b7ce6df80eb7037abf5b2f9fb02264ec_l3.png) i
i ![Rendered by QuickLaTeX.com [[Ag(SCN)_{4}]^{3-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-2f83b15e30eeb8ab92fee2c9b9ee508f_l3.png) , lepiej
, lepiej ![Rendered by QuickLaTeX.com [AgL_{2}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-653ae6ef2bd9b5d5f626c967173bebd5_l3.png) ,
, ![Rendered by QuickLaTeX.com [AgL_{3}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-bb3d4b906cc2a906363fbcc2a2c5234b_l3.png) i
i ![Rendered by QuickLaTeX.com [AgL_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-8d03e3546d34fce5468fd8fb95f155ad_l3.png) (L od ligand). W przypadku kwasów pisanie ładunku jonu jest raczej konieczne, a na pewno dużo bezpieczniejsze i zmniejszające szanse na popełnienie błędu – przy kompleksach jest to zbędne.
(L od ligand). W przypadku kwasów pisanie ładunku jonu jest raczej konieczne, a na pewno dużo bezpieczniejsze i zmniejszające szanse na popełnienie błędu – przy kompleksach jest to zbędne.
Aby wyznaczyć dokładną masę stopu, najlepiej rozplanować obliczenia tak, aby otrzymać w wyniku ![Rendered by QuickLaTeX.com [Zn^{2+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35e061eb7901f3a45496a7da69ca5696_l3.png) lub
lub ![Rendered by QuickLaTeX.com [[Zn(CN)_{4}]^{2-}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-d755ecd91d4afabc1505544b07519132_l3.png) (od tego momentu zapisywane jako
(od tego momentu zapisywane jako ![Rendered by QuickLaTeX.com [ZnL_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-707e2a76133c035227b8b705eb1c9b0d_l3.png) ). Dzięki temu, ponieważ znamy stosunek
). Dzięki temu, ponieważ znamy stosunek ![Rendered by QuickLaTeX.com [Zn^{2+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35e061eb7901f3a45496a7da69ca5696_l3.png) do
do ![Rendered by QuickLaTeX.com [ZnL_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-707e2a76133c035227b8b705eb1c9b0d_l3.png) , poznamy
, poznamy 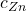 , więc także
, więc także 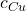 i będziemy w stanie obliczyć masę poszczególnych składników stopu, a więc też masę całej próbki.
i będziemy w stanie obliczyć masę poszczególnych składników stopu, a więc też masę całej próbki.
Wskazówka. Zacznijmy od tego, co wiemy. Nawet za urywki, początki obliczeń możesz dostać na Olchemie trochę punktów – bierz tylko pod uwagę czas, jaki spędzasz nad poszczególnymi poleceniami. Często mniej rozbudowane polecenia tuż przed „daniem głównym” mają na celu nakierować Cię na właściwy tok rozumowania – tak jest też i tym razem.
Zatem wyjdźmy od wyrażenia na stężenie całkowite cyjanków:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [CN^{-}] + [HCN] + 4[[Cu(CN)_{4}]^{3-}] + 4[[Zn(CN)_{4}]^{2-}] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e5ec31d2b6b19c5edbc43c0f4b191e6d_l3.png)
Czyli:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [L] + [HL] + 4[CuL_{4}] + 4[ZnL_{4}] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-490f75986e09c49b994add7db3af30c1_l3.png)
Stężenie analityczne cyjanków znamy – wynosi ono 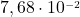 . Co więcej, znamy także stężenie wolnego liganda
. Co więcej, znamy także stężenie wolnego liganda ![Rendered by QuickLaTeX.com [L]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-79708952fc383a61d3c6dacd3d8ad11f_l3.png) . Wiemy bowiem, że:
. Wiemy bowiem, że:
![Rendered by QuickLaTeX.com $$ \frac{[ZnL_{4}]}{[Zn^{2+}]} = \frac{1}{10^{6}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-fba838163e88dcdd56d75037f1e109be_l3.png)
Podstawiając za ![Rendered by QuickLaTeX.com [ZnL_{4}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-707e2a76133c035227b8b705eb1c9b0d_l3.png) wyrażenie otrzymane z równania na
wyrażenie otrzymane z równania na 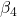 :
:
![Rendered by QuickLaTeX.com $$ \frac{\beta_{4 Zn}[Zn^{2+}][L]^{4}}{[Zn^{2+}]} = \frac{1}{10^{6}} $$ $$ \beta_{4 Zn}[L]^{4} = \frac{1}{10^{9}} $$ $$ [L]^{4} = \frac{1}{10^{6}\beta_{4 Zn}} $$ $$ [L] = (10^{6}\beta_{4 Zn})^{-\frac{1}{4}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b68229f9cfebe1c47184ef7d4b3d48c6_l3.png)
Wstawiamy dane (pamiętaj, że 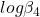 oznacza logarytm dziesiętny ze stałej niepomnożony przez
oznacza logarytm dziesiętny ze stałej niepomnożony przez 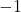 , w przeciwieństwie do np. wartości
, w przeciwieństwie do np. wartości 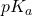 ):
):
![Rendered by QuickLaTeX.com $$ [L] = (10^{6} \cdot 10^{16,7})^{-\frac{1}{4}} = (10^{22,7})^{-\frac{1}{4}} = 10^{-\frac{22,7}{4}} \approx 2,11\cdot10^{-6} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ccc63dbafae2b0fd84895e75a4dfb306_l3.png)
Wróćmy do równania na 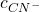 – skorzystajmy z tego, że mamy wyliczone
– skorzystajmy z tego, że mamy wyliczone ![Rendered by QuickLaTeX.com [L]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-79708952fc383a61d3c6dacd3d8ad11f_l3.png) . Przy użyciu wyrażeń na stałe komplesowania oraz na stałą dysocjacji podstawimy pozostałe składniki sumy, to znaczy:
. Przy użyciu wyrażeń na stałe komplesowania oraz na stałą dysocjacji podstawimy pozostałe składniki sumy, to znaczy:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [L] + [HL] + 4[CuL_{4}] + 4[ZnL_{4}] $$ $$ c_{CN^{-}} = [L] + \frac{[H^{+}][L]}{K_{a}} + 4[CuL_{4}] + 4[ZnL_{4}] $$ $$ c_{CN^{-}} = [L] + \frac{[H^{+}][L]}{K_{a}} + 4\beta_{4 Cu}[Cu^{+}][L]^{4} + 4\beta_{4 Zn}[Zn^{2+}][L]^{4} $$ $$ c_{CN^{-}} = (1 + \frac{[H^{+}]}{K_{a}})[L] + 4(\beta_{4 Cu}[Cu^{+}] + \beta_{4 Zn}[Zn^{2+}])[L]^{4} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3e4f5566832907c2602a4415f324f923_l3.png)
W równaniu zostały tylko dwie niewiadome – ![Rendered by QuickLaTeX.com [Zn^{2+]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0f9f4af17c121b5867a5f9e1f13a8278_l3.png) oraz
oraz ![Rendered by QuickLaTeX.com [Cu^{+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-2f7c673ebe7fa55dfdc1ac4bbb789ee8_l3.png) (
(![Rendered by QuickLaTeX.com [H^{+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0fb408d7e4e418ffa5b4f70a4bb67e15_l3.png) zostanie podstawione wg treści polecenia). Musimy więc „pozbyć się” tylko
zostanie podstawione wg treści polecenia). Musimy więc „pozbyć się” tylko ![Rendered by QuickLaTeX.com [Cu^{+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-2f7c673ebe7fa55dfdc1ac4bbb789ee8_l3.png) . Do tego przydadzą się obliczenia z podpunktu c):
. Do tego przydadzą się obliczenia z podpunktu c):
![Rendered by QuickLaTeX.com $$ {c_{Zn}} = 0,371{c_{Cu}} $$ $$ [Zn^{2+}] + [ZnL_{4}] = 0,371([Cu^{+}] + [CuL_{4}]) $$ $$ [Zn^{2+}](1 + \beta_{4 Zn}[L]^{4}) = 0,371[Cu^{+}](1 + \beta_{4 Cu}[L]^{4}) $$ $$ [Cu^{+}] = \frac{[Zn^{2+}]}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5accf82c6fd5d914d66c8a56e1692cf1_l3.png)
I podstawiamy:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = (1 + \frac{[H^{+}]}{K_{a}})[L] + 4(\beta_{4 Cu}[Cu^{+}] + \beta_{4 Zn}[Zn^{2+}])[L]^{4} $$ $$ c_{CN^{-}} = (1 + \frac{[H^{+}]}{K_{a}})[L] + 4\boldsymbol{(}\beta_{4 Cu}\frac{[Zn^{2+}]}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}[Zn^{2+}]\boldsymbol{)}[L]^{4} $$ $$ c_{CN^{-}} = (1 + \frac{[H^{+}]}{K_{a}})[L] + 4\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}[Zn^{2+}][L]^{4} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-2558fd4cd8f631bbbc5f23eefeb77a58_l3.png)
Oto finalne równanie, chociaż w postaci uwikłanej – należy tutaj dokonać jeszcze kilku prościutkich przekształceń:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = (1 + \frac{[H^{+}]}{K_{a}})[L] + 4\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}[Zn^{2+}][L]^{4} $$ $$ c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L] = 4\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}[Zn^{2+}][L]^{4} $$ $$ [Zn^{2+}] = \frac{c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]}{4\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}[L]^{4}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7861686f6942834fed4ddecb609d1f5d_l3.png)
Dla czytelności:
![Rendered by QuickLaTeX.com $$ [Zn^{2+}] = \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}\boldsymbol{)}^{-1} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b2a932e5db31187042b258c8cff0420f_l3.png)
Podstawmy dane; dla 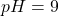 :
:
![Rendered by QuickLaTeX.com [Zn^{2+}] = \boldsymbol{(}7,68\cdot10^{-2} - (1 + \frac{10^{-9}}{10^{-9,36}})\cdot(2,11\cdot10^{-6})\boldsymbol{)}\cdot \\ \cdot\boldsymbol{(}4\cdot(2,11\cdot10^{-6})^{4}\cdot\boldsymbol{(}\frac{10^{30,3}}{0,371} \frac{(1 + 10^{16,7}\cdot(2,11\cdot10^{-6})^{4})}{(1 + 10^{30,3}\cdot(2,11\cdot10^{-6})^{4})} + 10^{16,7}\boldsymbol{)}\boldsymbol{)}^{-1} \approx 7,12\cdot10^{-3}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-24b050f36afafc5bb560a4b9abce9948_l3.png)
Dla 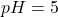 :
:
![Rendered by QuickLaTeX.com [Zn^{2+}] = \boldsymbol{(}7,68\cdot10^{-2} - (1 + \frac{10^{-5}}{10^{-9,36}})\cdot(2,11\cdot10^{-6})\boldsymbol{)}\cdot \\ \cdot\boldsymbol{(}4\cdot(2,11\cdot10^{-6})^{4}\cdot\boldsymbol{(}\frac{10^{30,3}}{0,371} \frac{(1 + 10^{16,7}\cdot(2,11\cdot10^{-6})^{4})}{(1 + 10^{30,3}\cdot(2,11\cdot10^{-6})^{4})} + 10^{16,7}\boldsymbol{)}\boldsymbol{)}^{-1} \approx 2,64\cdot10^{-3}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-24193fbdd74e817410f95b407a2ba607_l3.png)
W tym momencie zatrzymamy się. Otrzymaliśmy idiotycznie wręcz złożony wzór na ![Rendered by QuickLaTeX.com [Zn^{2+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35e061eb7901f3a45496a7da69ca5696_l3.png) . Jest on ścisły w warunkach zadania – nie zostało zastosowane żadne przybliżenie. Wyprowadzanie takich wzorów nie ma jednak większego sensu – zajmuje zbyt wiele czasu, aby móc je jakkolwiek zastosować, zwłaszcza w warunkach Olimpiady. Przyjrzyjmy się więc otrzymanemu równaniu i sprawdźmy, jakie jego elementy można uznać za „zbędne”.
. Jest on ścisły w warunkach zadania – nie zostało zastosowane żadne przybliżenie. Wyprowadzanie takich wzorów nie ma jednak większego sensu – zajmuje zbyt wiele czasu, aby móc je jakkolwiek zastosować, zwłaszcza w warunkach Olimpiady. Przyjrzyjmy się więc otrzymanemu równaniu i sprawdźmy, jakie jego elementy można uznać za „zbędne”.
Aby być w stanie to zrobić, musimy najpierw oszacować wartość wyrażenia ![Rendered by QuickLaTeX.com [L]^{4}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3100c406fe195e79eda39a3dab02d34e_l3.png) . Wynosi ono w przybliżeniu
. Wynosi ono w przybliżeniu 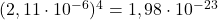 . Możemy zatem zapisać:
. Możemy zatem zapisać:
![Rendered by QuickLaTeX.com $$ 1 \boldsymbol{\gg} \beta_{4 Zn}[L]^{4} \approx 9,93\cdot10^{-7} $$ $$ 1 \boldsymbol{\ll} \beta_{4 Cu}[L]^{4} \approx 3,95\cdot10^{7} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-42989880ccd18bbbbe688238e27714aa_l3.png)
A także:
![Rendered by QuickLaTeX.com $$ \frac{1}{[L]^{4}} \approx 5,05\cdot10^{22} \boldsymbol{\gg} \beta_{4 Zn} \approx 5,01\cdot10^{16} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3c7a559d5f5e00c2d79ff5bb7bcba09e_l3.png)
W konsekwencji tych obserwacji zapisać można:
![Rendered by QuickLaTeX.com $$ [Zn^{2+}] = \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{(1 + \beta_{4 Zn}[L]^{4})}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}\boldsymbol{)}^{-1} \approx $$ $$ \approx \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{1}{(1 + \beta_{4 Cu}[L]^{4})} + \beta_{4 Zn}\boldsymbol{)}\boldsymbol{)}^{-1} \approx $$ $$ \approx \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\boldsymbol{(}\frac{\beta_{4 Cu}}{0,371} \frac{1}{\beta_{4 Cu}[L]^{4}} + \beta_{4 Zn}\boldsymbol{)}\boldsymbol{)}^{-1} = $$ $$ = \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\boldsymbol{(}\frac{1}{0,371} \frac{1}{[L]^{4}} + \beta_{4 Zn}\boldsymbol{)}\boldsymbol{)}^{-1} \approx $$ $$ \approx \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}4[L]^{4}\frac{1}{0,371} \frac{1}{[L]^{4})}\boldsymbol{)}^{-1} = $$ $$ = \boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)}\cdot\boldsymbol{(}\frac{4}{0,371}\boldsymbol{)}^{-1} $$ $$ [Zn^{2+}] = \frac{0,371}{4}\cdot\boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4eef73d03fd5b9724eec4901e92ba34c_l3.png)
Cały czas korzystamy z prostego spostrzeżenia, że jeżeli 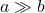 , to
, to 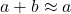 . Korzystając z takiego wzoru, otrzymujemy:
. Korzystając z takiego wzoru, otrzymujemy:
![Rendered by QuickLaTeX.com $$ pH = 9:\:[Zn^{2+}] = \frac{0,371}{4}\cdot\boldsymbol{(}7,68\cdot10^{-2} - ((1 + \frac{10^{-9}}{10^{-9,36}})\cdot2,11\cdot10^{-6})\boldsymbol{)} \approx 7,12\cdot10^{-3} $$ $$ pH = 5:\:[Zn^{2+}] = \frac{0,371}{4}\cdot\boldsymbol{(}7,68\cdot10^{-2} - ((1 + \frac{10^{-5}}{10^{-9,36}})\cdot2,11\cdot10^{-6})\boldsymbol{)} \approx 2,64\cdot10^{-3} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7748d6e9cba7a594b0bdd6fb0bf5f369_l3.png)
Widzimy, że przy dokładności do trzech cyfr znaczących błąd przybliżenia jest niezauważalny – uproszczenia były zatem uprawnione.
Co jednak może być zupełnie zaskakujące, zwłaszcza w kontekście tego, że spędziłem dobre dwie godziny na pisaniu odpowiedzi na ten podpunkt i wklepywaniu jej do LaTeXa, do uproszczonego wzoru mogliśmy dojść praktycznie na samym początku obliczeń. Zauważmy:
![Rendered by QuickLaTeX.com $$ [Zn^{2+}] = 10^{6}[ZnL_{4}] \implies [Zn^{2+}] \gg [ZnL_{4}] \implies $$ $$ \implies [Zn^{2+}] + [ZnL_{4}] \approx [Zn^{2+}] \implies [Zn^{2+}] \approx c_{Zn} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-c7653654eeb938155d7feb747638de7d_l3.png)
Stosunek formy skompleksowanej do nieskompleksowanej obliczyć należy także dla miedzi:
![Rendered by QuickLaTeX.com $$ \beta_{4 Cu} = \frac{[CuL_{4}]}{[Cu^{+}][L]^{4}} $$ $$ \frac{[CuL_{4}]}{[Cu^{+}]} = \beta_{4 Cu}[L]^{4} \approx 3,95\cdot10^{7} \implies [CuL_{4}] \gg [Cu^{+}]$$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f1fed0eef2f6584e8f03d2693fc9a0e5_l3.png)
I dalej tak jak powyżej, tylko że „na odwrót”, czyli ostatecznie ![Rendered by QuickLaTeX.com [CuL_{4}] \approx c_{Cu}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-605046010283cfe924e93bd30132867c_l3.png) .
.
Zatem, wychodząc z wyprowadzonego na początku:
![Rendered by QuickLaTeX.com $$ c_{CN^{-}} = [L] + [HL] + 4[CuL_{4}] + 4[ZnL_{4}] $$ $$ c_{CN^{-}} = [L] + \frac{[H^{+}][L]}{K_{a}} + 4[CuL_{4}] + 4[ZnL_{4}] $$ $$ c_{CN^{-}} = [L] + \frac{[H^{+}][L]}{K_{a}} + 4 c_{Cu} + 4[ZnL_{4}] $$ $$ c_{CN^{-}} = [L] + \frac{[H^{+}][L]}{K_{a}} + 4c_{Cu} + 4\beta_{4 Zn}[L]^{4}[Zn^{2+}] $$ $$ c_{CN^{-}} = [L](1+ \frac{[H^{+}]}{K_{a}}) + \frac{4}{0,371}c_{Zn} + 4\beta_{4 Zn}[L]^{4}c_Zn $$ $$ c_{CN^{-}} - [L](1+ \frac{[H^{+}]}{K_{a}}) = \frac{4}{0,371}c_{Zn} $$ $$ c_{Zn} = \frac{0,371}{4}\cdot\boldsymbol{(}c_{CN^{-}} - (1 + \frac{[H^{+}]}{K_{a}})[L]\boldsymbol{)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-024070349c5916cfc00c8a520cc7fc1c_l3.png)
Przedostatnie przejście na mocy tego, że ![Rendered by QuickLaTeX.com \beta_{4 Zn}[L]^{4} \approx 9,93\cdot10^{-7} \approx 0](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-64d2b4e8e3a7bf066022a7a844b9904d_l3.png) . Ponieważ
. Ponieważ ![Rendered by QuickLaTeX.com c_{Zn} \approx [Zn^{2+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3ad1c180da049cdbde91b8c174880ee5_l3.png) , otrzymany uproszczony wzór jest identyczny z poprzednim, mimo że uproszczenia przeprowadzane były w inny sposób.
, otrzymany uproszczony wzór jest identyczny z poprzednim, mimo że uproszczenia przeprowadzane były w inny sposób.
Wskazówka. Jeśli chodzi o takie uproszczenia, sztywno ustalone reguły istnieją tylko w niektórych przypadkach, np. jeżeli chcemy uznać drugą dysocjację kwasu dwuprotonowego za pomijalną. Stety lub niestety, ale trzeba kierować się zdrowym rozsądkiem – brać pod uwagę oczekiwaną dokładność wyniku i działania, jakim poddawany jest uproszczony człon równania. Tutaj, skoro pożądana dokładność to trzy cyfry znaczące (jest to standardowa dokładność, jeżeli w poleceniu nie napisano inaczej), to możemy uznać, że składniki sumy mniejsze o co najmniej trzy rzędy wielkości od największego składnika są pomijalne. Trochę inaczej byłoby, gdybyśmy np. podnosili upraszczane wyrażenia do potęgi albo brali z nich logarytm. Warto wspomnieć na przykład o wzorze 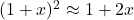 , gdy
, gdy 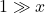 (rozwinięcie wzoru skróconego mnożenia z pominięciem
(rozwinięcie wzoru skróconego mnożenia z pominięciem 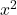 , już kompletnie pomijalnego). Nie warto się tu już dalej rozpisywać, inne uproszczenia pokazane zostaną kiedy indziej, na przykładach. Tak czy inaczej, należy się tu po prostu wykazać logicznym myśleniem.
, już kompletnie pomijalnego). Nie warto się tu już dalej rozpisywać, inne uproszczenia pokazane zostaną kiedy indziej, na przykładach. Tak czy inaczej, należy się tu po prostu wykazać logicznym myśleniem.
Musimy jeszcze, w ramach formalności, dokończyć rozwiązywanie zadania. Znamy ![Rendered by QuickLaTeX.com [Zn^{2+}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35e061eb7901f3a45496a7da69ca5696_l3.png) , a że
, a że ![Rendered by QuickLaTeX.com [Zn^{2+}] \approx c_{Zn}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-dabc0a0e9ffd8ed101abb0a72535b5a8_l3.png) , to:
, to:
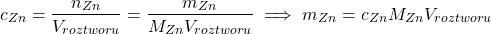
Z podpunktu a):
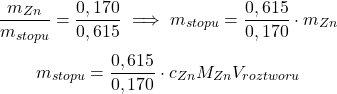
Podstawmy dane – dla 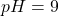 :
:
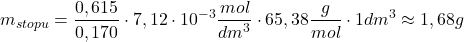
Dla 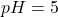 :
:
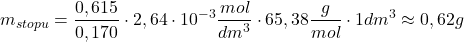
f) Jakie musiałoby być KSo?
Cały ten podpunkt jest bardzo grubymi niciami szyty i w zasadzie mogłoby (a nawet powinno) go tu nie być – ma jednak istotną funkcję dydaktyczną, o której zaraz.
Żeby obliczenia z punktu e) były poprawne, musimy założyć, że stężenia analityczne cyjanków, miedzi i cynku są stałe i że stężenie analityczne cyjanków jest nam znane – czyli, że nie wytrącają się osady, ani że nie wydzielają się gazy. Jeżeli nie wytrącają się osady, to znaczy, że żadne 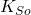 nie jest przekroczone – sprawdźmy zatem, jakie musiałoby być
nie jest przekroczone – sprawdźmy zatem, jakie musiałoby być ![Rendered by QuickLaTeX.com K_{So\:Zn_{3}[Cu(CN)_{4}]_{2}}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5ecbd91799057cd57dbb030c212a8bcb_l3.png) , żeby wszystko się zgadzało.
, żeby wszystko się zgadzało.
Na podstawie uproszczeń omówionych w podpunkcie e):
![Rendered by QuickLaTeX.com $$ K_{So\:Zn_{3}[Cu(CN)_{4}]_{2}} = ([Zn^{2+}]_{max})^{3}([[Cu(CN)_{4}]^{3-}]_{max})^{2} \approx (c_{Zn max})^{3} \cdot (c_{Cu max})^{2} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b4527926db79a6eadba2cbe898ad4e2e_l3.png)
Na podstawie podpunktu c):
![Rendered by QuickLaTeX.com $$ K_{So\:Zn_{3}[Cu(CN)_{4}]_{2}} = (c_{Zn max})^{3} \cdot (c_{Cu max})^{2} \approx (c_{Zn max})^{3} \cdot (\frac{c_{Zn max}}{0,371})^{2} = \frac{(c_{Zn max})^{5}}{0,371^{2}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-39139a97cdfa46f36bed2f8f42892340_l3.png)
Jeżeli nie jest przekroczone, to znaczy, że:
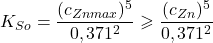
Po podstawieniu, dla 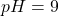 otrzymujemy
otrzymujemy ![Rendered by QuickLaTeX.com K_{So\:Zn_{3}[Cu(CN)_{4}]_{2}} \geqslant 1,33\cdot10^{-10}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ebef1ec8e1ccd7b574f72f1bc3bb3c98_l3.png) , natomiast dla
, natomiast dla ![Rendered by QuickLaTeX.com pH = 5\:\:K_{So Zn_{3}[Cu(CN)_{4}]_{2}} \geqslant 9,31\cdot10^{-13}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b3dbdc00ab30c9cceb1f3caeb9a28e39_l3.png) .
.
Zatem dla ![Rendered by QuickLaTeX.com K_{So\:Zn_{3}[Cu(CN)_{4}]_{2}}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-18b0d82c1310dbba7a50d365958c1ad6_l3.png) musi być równe lub większe
musi być równe lub większe 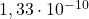 . I co dalej? Cóż, możemy co najwyżej przeliczyć to na masę – okaże się wtedy, że w litrze wody rozpuszczać musiałoby się przynajmniej
. I co dalej? Cóż, możemy co najwyżej przeliczyć to na masę – okaże się wtedy, że w litrze wody rozpuszczać musiałoby się przynajmniej 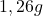 tego związku.
tego związku.
Wskazówka. I co teraz biedny rozwiązujący zadanie ma zrobić? Ano nic. Brak danych, do których można porównać otrzymany wynik. Brak możliwości udzielenia ścisłej odpowiedzi. Jest to przybliżenie kolejnej z cech Olimpiady – dość często pojawiających się błędów w zadaniach, zwłaszcza w ich części obliczeniowej. Ja mogę Ci tylko zdradzić, że tego typu związki kompleksowe zazwyczaj strącają się (są bardzo słabo rozpuszczalne) ze w zasadzie wszystkimi kationami, poza kationami pierwszej grupy układu okresowego (oraz 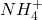 ). Zatem obliczone w punkcie e) wartości są mało prawdopodobne. Rozwiązując to zadanie na czas należałoby udzielić takiej właśnie, słabej i nieścisłej odpowiedzi, albo po prostu zignorować dalszą część polecenia.
). Zatem obliczone w punkcie e) wartości są mało prawdopodobne. Rozwiązując to zadanie na czas należałoby udzielić takiej właśnie, słabej i nieścisłej odpowiedzi, albo po prostu zignorować dalszą część polecenia.
Adnotacja. Polecenie to pokazuje, że rozbudowane obliczenia z podpunktu wcześniejszego w zasadzie nie mają sensu fizycznego – i rzeczywiście tak jest. Podpunkt e) miał na celu parę rzeczy – pokazać, jak należy stosować podstawienia jednych wzorów do drugich, wykazać, że uproszczenia są konieczne i zaprezentować, jak należy je stosować etc. Niestety, zadania z chemii analitycznej rzadko kiedy są interesujące i kreatywne, natomiast w formule olimpijskiej dość ciężko jest pokazać kilka zagadnień naraz. Należy więc troszkę nagiąć rzeczywistość, jak miało to miejsce powyżej. Ocenę takiej praktyki pozostawiam Tobie. Zresztą, wszystko to wina „pewnego niezbyt błyskotliwego chemika” – zrzucam z siebie odpowiedzialność.
g) Jak rozdzielić miedź i cynk?
Wskazówka. Ten podpunkt to typowy „nabijacz punktów” – pytanie, na które jest w stanie odpowiedzieć każdy, ale nie każdy to robi, przez brak czasu czy nieuwagę. Trzeba po prostu na nie uważać. Czasem, gdy nie masz już czasu na zadanie lub zwyczajnie nie potrafisz go rozwiązać, takie polecenie może przynieść niezbędne punkciki – można je wykonać osobno, nie tykając nawet poprzednich podpunktów.
Aby rozdzielić zawarty w próbce A cynk od miedzi (są one obecne w postaci 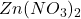 oraz
oraz 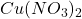 ), wystarczy np. rozpuścić próbkę w wodzie, a następnie doprowadzić
), wystarczy np. rozpuścić próbkę w wodzie, a następnie doprowadzić 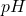 do bardzo wysokich wartości, chociażby stężonym
do bardzo wysokich wartości, chociażby stężonym 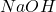 . Początkowo strącą się, trudne do rozdzielenia,
. Początkowo strącą się, trudne do rozdzielenia, 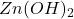 i
i 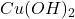 . Następnie, przy odpowiednio wysokim stężeniu jonów
. Następnie, przy odpowiednio wysokim stężeniu jonów 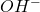 , wodorotlenek cynku zaczyna być kompleksowany do postaci jonów cynkanowych
, wodorotlenek cynku zaczyna być kompleksowany do postaci jonów cynkanowych ![Rendered by QuickLaTeX.com [Zn(OH)_{4}]^{2-}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13ae0fab03779dce8218f0f1d9e60cb3_l3.png) , które przechodzą do roztworu. Wodorotlenek miedzi(II) nie reaguje w ten sposób.
, które przechodzą do roztworu. Wodorotlenek miedzi(II) nie reaguje w ten sposób.
Oczywiście, inne poprawne metody również są dopuszczalne i w pełni punktowane. Przykładowo, dodanie do roztworu próbki A nadmiaru jonów jodkowych poskutkowałoby zredukowaniem miedzi(II) i wytrąceniem jodku miedzi(I) wedle równania:
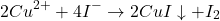
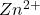 pozostałyby w roztworze.
pozostałyby w roztworze.
Uff, koniec, dziękuję za uwagę.
Trzymajcie się, do następnego wpisu ^^ .