Krystalografia – część 1/2
Poziom Olimpiady Chemicznej rośnie z roku na rok – finałowe zadania sprzed kilkunastu lat teraz nadają się na pierwszy/drugi etap! Sprawia to, że nawet doświadczeni zawodnicy muszą stale poszerzać swoją wiedzę. Jednym z zagadnień, których wymagana jest coraz bardziej szczegółowa znajomość, jest krystalografia, która często stanowi problem dla nowych pasjonatów Olimpiady. Powody są różne: brak przystępnej literatury, która tłumaczyłaby wyczerpująco ten dział chemii, trudności z wyobrażeniem sobie i samodzielnym zrozumieniem niektórych zagadnień albo brak wprawy w schemacie zadań. Dlatego właśnie krystalografii poświęcimy ten i nie tylko ten wpis.
Zanim przejdziemy dalej, musimy zdać sobie sprawę z tego, jak ważna jest obecnie krystalografia. Zadebiutowała na finale 56. Olchemu, w bardzo prymitywnej postaci – zadanko dało się rozwiązać bez specjalistycznej wiedzy, gdyż wszystko było wytłumaczone w jego treści. Następnie 5 lat względnej ciszy, krystalografia przewijała się czasem w folderach, aż nagle – od 61. edycji została ona stałym elementem finałów, a od 64. edycji – również drugich etapów. W tegorocznym (68.) finale, ponad 80% punktów w zadaniu 2. było do zdobycia właśnie za krystalografię; przy tym poziom trudności tego zadania jeszcze 3 lata wcześniej uznano by za niewyobrażalny. Ten wpis będzie wprowadzeniem w podstawy i potrzebne definicje. Warto go przeczytać, nawet jeśli myślisz, że dobrze znasz ten temat – może dowiesz się czegoś nowego (np. jak nazywa się „kreska nad liczbami” we wskaźnikach Millera).
Czym jest kryształ?
Jedną z pierwszych osób, które naukowo analizowały ciała krystaliczne, był Christiaan Huygens, który w siedemnastym wieku badał m.in. kalcyt. Zauważył on, że minerał ten załamuje światło w różny sposób, w zależności od kierunku wiązki światła a także, że kryształy różnego rozmiaru zachowują te same elementy symetrii. Doszedł więc do wniosku, że musi istnieć pewna podstawowa jednostka, która tworzy ciało krystaliczne i nadaje mu wspomniane właściwości. Jednostka ta nazywana jest komórką elementarną. Komórka elementarna ma kształt równoległościanu, który jest w stanie w nieskończoność pokryć przestrzeń przez translację, czyli przesunięcie o wektor (to tłumaczy, dlaczego podstawą komórki elementarnej nie może być trójkąt lub pięciokąt).
Zatrzymajmy się na chwilę i przedstawmy koncept komórki elementarnej w dwóch wymiarach:

Mamy tutaj siatkę niebieskich kul – od razu widać, że powtarzającym się, najprostszym elementem będzie romb złożony z czterech takich kul. Tę komórkę opisują dwie podstawowe wielkości – długość krawędzi rombu oraz kąt wewnętrzny (w tym przypadku kąt o mniejszej mierze. Gdyby komórką był równoległobok, opisywałaby go dodatkowa wielkość – długość drugiego boku. Pomimo tego, że komórkę rysuje się przy pomocy czterech kół, to w rzeczywistości zawiera ona jedno koło – każdy punkt na przecięciu linii należy po równo do czterech komórek, więc cztery ćwiartki kul sumują się do jednej kuli.
Na pierwszym rysunku widzimy również czarne linie, które tworzą sieć przestrzenną. Wyznaczają one ramy komórki elementarnej. Sieć można zdefiniować jako ułożenie punktów w przestrzeni w taki sposób, że wszystkie punkty są identyczne – mają takie samo otoczenie. Sieć krystalograficzna to natomiast sieć przestrzenna obsadzona atomami.
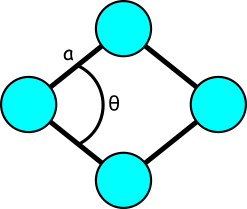
Dopóki jesteśmy jeszcze w dwóch wymiarach, warto zapamiętać znaczenie liczby koordynacyjnej – jest to liczba „najbliższych sąsiadów” danego atomu. W przykładzie powyżej każda kula ma 4 „sąsiadów”, oddalonych o tę samą, najmniejszą odległość.
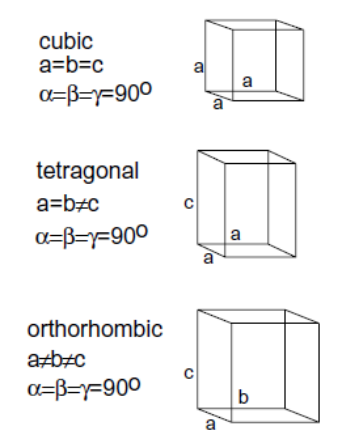
Układy krystalograficzne
Gdy przechodzimy do trzech wymiarów, pojawia się więcej obiektów, którymi można wypełnić przestrzeń, dokonując wyłącznie translacji. Wyróżniamy siedem podstawowych układów krystalograficznych, które opisują rodziny równoległościanów, których kształt mogą przybierać komórki elementarne. Układy te prawie zawsze opisuje się w następujący sposób: trzy krawędzi wychodzące z jednego punktu nazywa się  ,
, 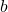 i
i  , kąt pomiędzy
, kąt pomiędzy 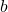 i
i  nazywa się
nazywa się 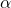 , pomiędzy
, pomiędzy  i
i  –
– 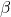 , a pomiędzy
, a pomiędzy  i
i 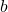 –
– 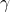 . Następnie opisuje się długości boków i wartości kątów.
. Następnie opisuje się długości boków i wartości kątów.
Układy krystalograficzne:
- Regularny – sześcian. Najczęściej pojawiający się na olimpiadzie układ.
- Tetragonalny – prostopadłościan, którego podstawą jest kwadrat, a wysokość nie jest równa długości krawędzi podstawy.
- Rombowy* – prostopadłościan, którego podstawą jest prostokąt niebędący kwadratem, a wysokość nie jest równa żadnej z długości krawędzi podstawy.
*Nie, nie pomyliłem nazw – należy uważać, tłumacząc nazwy układów z angielskiego na polski, ponieważ można wtedy łatwo pomylić układ rombowy z trygonalnym. - Trygonalny – równoległościan o wszystkich krawędziach równych i trzech identycznych kątach, nierównych 90°.
- Heksagonalny – równoległościan, którego podstawą jest romb o kątach 120° i 60°, ściany są prostopadłe do podstawy, a wysokość nie jest równa długościom krawędzi podstawy.
- Jednoskośny – równoległościan o trzech różnych krawędziach i jednym kącie nierównym 90°.
- Trójskośny – równoległościan o trzech różnych krawędziach i trzech różnych kątach różnych od 90°.
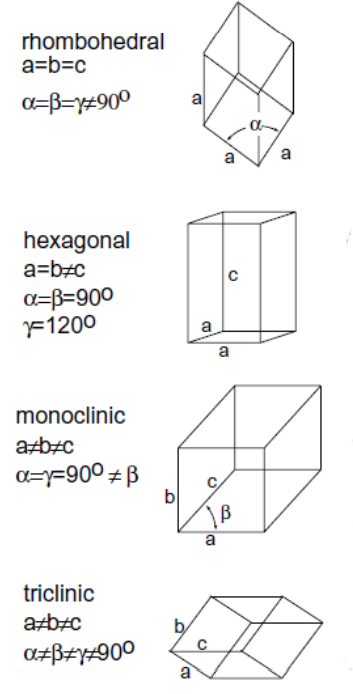
Z perspektywy Olimpiady najważniejsze są układy regularny i heksagonalny; tylko one pojawiają się w zadaniach, ale to nie znaczy, że nie warto kojarzyć też reszty.
Sieci Bravais’go
Formalnie sieć Bravais’go to generacja dodatkowych punktów przez nałożenie na podstawową sieć przestrzenną, sieć danego układu przesuniętą o wektor, który można określić jako 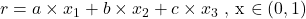 , przy czym
, przy czym  ,
,  i
i  to oczywiście wektory o długości odpowiednich boków i do nich równoległe. Może się wydawać, że taka operacja daje nieskończoność opcji, jednak tak naprawdę istnieją tylko 4 typy sieci Bravais’go. Dlaczego? Bo bierzemy pod uwagę jedynie struktury, w których dochodzi do „centrowania” komórki – generacji punktów w środku przestrzeni lub na środkach ścian (wygenerowanie punktów w innych miejscach prowadzi do utworzenia innego układu krystalograficznego). Mamy więc cztery sieci:
to oczywiście wektory o długości odpowiednich boków i do nich równoległe. Może się wydawać, że taka operacja daje nieskończoność opcji, jednak tak naprawdę istnieją tylko 4 typy sieci Bravais’go. Dlaczego? Bo bierzemy pod uwagę jedynie struktury, w których dochodzi do „centrowania” komórki – generacji punktów w środku przestrzeni lub na środkach ścian (wygenerowanie punktów w innych miejscach prowadzi do utworzenia innego układu krystalograficznego). Mamy więc cztery sieci:
- prymitywna
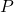 – bez dodatkowych punktów;
– bez dodatkowych punktów; - przestrzennie centrowana
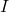 – posiada dodatkowy punkt w środku komórki;
– posiada dodatkowy punkt w środku komórki; - ściennie centrowana
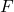 – posiada sześć dodatkowych punktów, jeden pośrodku każdej ściany;
– posiada sześć dodatkowych punktów, jeden pośrodku każdej ściany; - o centrowanej podstawie
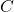 – posiada dwa dodatkowe punkty na środkach przeciwległych ścian.
– posiada dwa dodatkowe punkty na środkach przeciwległych ścian.
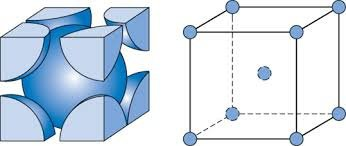
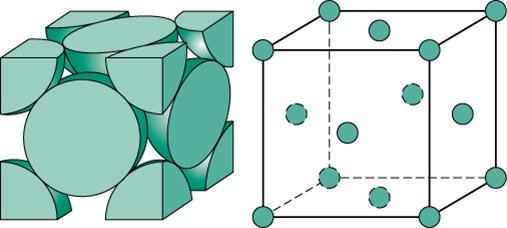
Zauważmy, że konsekwencją dodania punktów jest oczywiście zwiększenie liczby atomów w komórce. Sieć prymitywna posiada 8 atomów, z czego każdy znajduje się tylko w 1/8 w komórce; po wymnożeniu otrzymujemy jeden atom. Sieć przestrzennie centrowana w porównaniu do prymitywnej ma dodatkowy atom, w całości należący do komórki, więc razem zawiera dwa atomy. Sieć ściennie centrowana posiada 6 dodatkowych atomów w połowie należących do komórki, więc zawiera łącznie cztery atomy, a sieć o centrowanej podstawie posiada tylko 2 takie w połowie należące do niej atomy, więc po zsumowaniu zawiera dwa atomy.
Biorąc pod uwagę wcześniejsze informacje może nam się teraz wydawać, że istnieje 28 sieci Bravais’go (7 układów, każdy w 4 typach), ale w rzeczywistości jest ich tylko 14. Zastosowanie centrowań na niektórych komórkach prowadzi do utworzenia nowej komórki o innych stosunków boków, np. centrowanie ścienne sieci tetragonalnej daje sieć tetragonalną prymitywną o innym stosunku długości boków. Mamy więc każdy układ w sieci 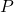 oraz regularny
oraz regularny 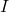 i
i 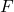 , tetragonalny
, tetragonalny 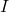 , rombowy
, rombowy 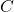 ,
, 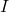 i
i 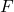 oraz jednoskośny
oraz jednoskośny 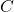 . Dla nas najważniejsze będą układy regularny ściennie i przestrzennie centrowany.
. Dla nas najważniejsze będą układy regularny ściennie i przestrzennie centrowany.
Wskaźniki Millera – punkty i wektory
Omówiliśmy najważniejsze sposoby opisu uporządkowania atomów w krysztale. Możemy zauważyć, że opisywanie konkretnych punktów w komórce elementarnej staje się coraz trudniejsze. To nie problem, gdyż w krystalografii dysponujemy notacją pozwalającą opisywać punkty, kierunki i płaszczyzny.
Wskaźniki Millera to po prostu prezentacja współrzędnych 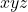 , z małymi haczykami. Wartości
, z małymi haczykami. Wartości  ,
, 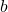 ,
,  uznajemy za jednostkowe odpowiednio na osiach
uznajemy za jednostkowe odpowiednio na osiach 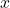 ,
, 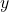 ,
,  (a oficjalnie to mamy wartości
(a oficjalnie to mamy wartości 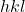 , które różnią się nieco od zwykłych współrzędnych). Rysując komórkę elementarną, za początek układu współrzędnych obieramy punkt na sieci „najbardziej oddalony” od obserwatora, czyli z tyłu, po lewej, na dolnej podstawie – ma on współrzędne, które normalnie zapisalibyśmy jako
, które różnią się nieco od zwykłych współrzędnych). Rysując komórkę elementarną, za początek układu współrzędnych obieramy punkt na sieci „najbardziej oddalony” od obserwatora, czyli z tyłu, po lewej, na dolnej podstawie – ma on współrzędne, które normalnie zapisalibyśmy jako 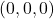 , jednak w tej notacji zapisujemy po prostu
, jednak w tej notacji zapisujemy po prostu 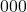 . Teraz zobaczmy, jakie są współrzędne punktów w układzie regularnym:
. Teraz zobaczmy, jakie są współrzędne punktów w układzie regularnym:
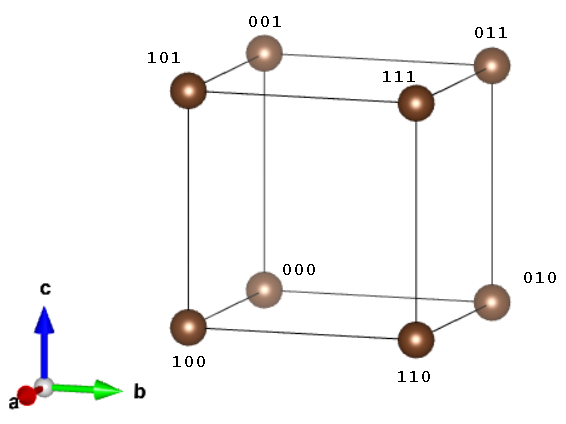
W układzie regularnym centrowanym przestrzennie środkowy punkt ma współrzędne 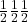 . W układzie regularnym ściennie centrowanym występują dodatkowe punkty o współrzędnych
. W układzie regularnym ściennie centrowanym występują dodatkowe punkty o współrzędnych 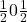 ,
, 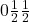 ,
,  ,
, 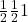 ,
, 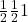 ,
, 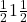 .
.
Wiemy już, jak nazywać punkty, więc nie będziemy mieli żadnych trudności z wektorami. Wektor opisujemy tak samo jak punkt, który łączy go z punktem 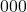 .
.
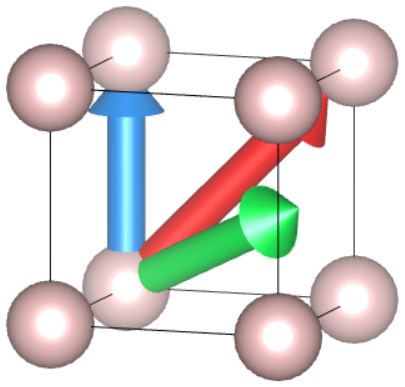
Tak więc niebieski wektor łączy punkt 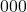 z
z 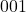 , więc opisujemy go w kwadratowych nawiasach jako
, więc opisujemy go w kwadratowych nawiasach jako ![Rendered by QuickLaTeX.com [001]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-eadfece730d28976d2880143aa00633d_l3.png) . Analogicznie, czerwony to
. Analogicznie, czerwony to ![Rendered by QuickLaTeX.com [011]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-6c9ab2157dda74c1dcf7a422a2ec688d_l3.png) , a zielony, który kończy się na środku ściany, to
, a zielony, który kończy się na środku ściany, to ![Rendered by QuickLaTeX.com [\frac{1}{2}1\frac{1}{2}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a22b67fc16ff9d41d7ad13da7cb69df0_l3.png) , prawda? Nie do końca. Konwencja zakłada, że nie korzystamy z ułamków podając wartości hkl, wektorów lub płaszczyzn. Wymnażamy więc do liczb całkowitych – wektor zielony to
, prawda? Nie do końca. Konwencja zakłada, że nie korzystamy z ułamków podając wartości hkl, wektorów lub płaszczyzn. Wymnażamy więc do liczb całkowitych – wektor zielony to ![Rendered by QuickLaTeX.com [121]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-05d1df33d665dbbbe4718bfde613316f_l3.png) .
.
Pamiętaj, że nazywając tak wektor, nie mówimy nic o jego punkcie przyłożenia, tak więc wektor czerwony może np. wychodzić z punktu 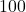 i prowadzić do punktu
i prowadzić do punktu  – cały czas pozostaje tym samym wektorem (zauważmy, że jest on nawet różnicą wektorów
– cały czas pozostaje tym samym wektorem (zauważmy, że jest on nawet różnicą wektorów ![Rendered by QuickLaTeX.com [100]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-8a413b2665538e5dac2bea6fa2f18013_l3.png) i
i ![Rendered by QuickLaTeX.com [111]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b01e4678f3d3cc4e33025ef3c80c4b57_l3.png) ).
).
Spójrzmy jeszcze na jeden przykład – co się dzieje, kiedy zwrot jest odwrócony?
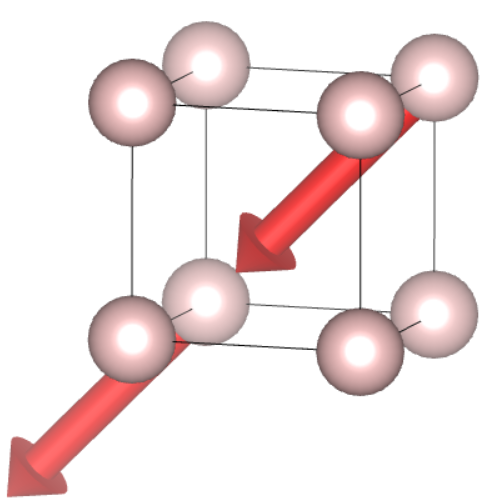
Jak już określiliśmy, oba wektory opiszemy tak samo, bo mają ten sam kierunek, wartość i zwrot. Patrząc na wektor wychodzący z punktu 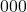 i myśląc czysto matematycznie, można podać odpowiedź
i myśląc czysto matematycznie, można podać odpowiedź ![Rendered by QuickLaTeX.com [0\:\text{-}1\:\text{-}1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-798a20f6323aa97616e32690672729da_l3.png) , bo wektor skierowany jest w wartość -1 na osi
, bo wektor skierowany jest w wartość -1 na osi 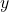 i
i  – jest to merytorycznie poprawne. Pozostaje kwestia zapisu, zamiast minusa stosujemy makron, czyli kreseczkę nad liczbą.
– jest to merytorycznie poprawne. Pozostaje kwestia zapisu, zamiast minusa stosujemy makron, czyli kreseczkę nad liczbą. ![Rendered by QuickLaTeX.com \hkl[0-1-1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-31a4ddb75a3c2372269294b9b8f9a85f_l3.png) .
.
Mam nadzieję, że do tej pory wszystko jest zrozumiałe. Jeżeli wciąż masz problem z podpisaniem wektorów, sprawdź sobie parę obrazków w Internecie. Nie ma w tym przypadku lepszej metody niż nauka na przykładach.
W układzie heksagonalnym nie ma większej filozofii w kwestii wektorów, zobaczmy na obrazek:
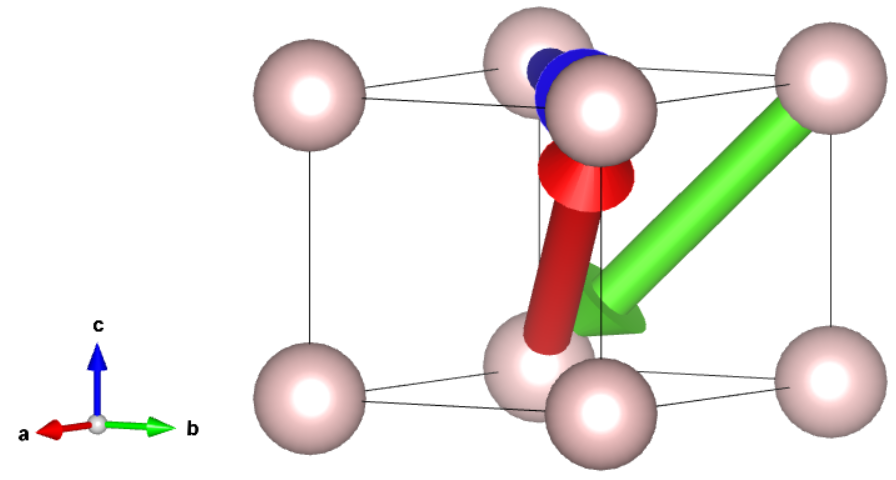
Wektor czerwony to ![Rendered by QuickLaTeX.com \hkl[1 1 1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e2747355e723103136b4bde2d5369142_l3.png) , zielony to
, zielony to ![Rendered by QuickLaTeX.com \hkl[0 -1 -1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b0e9fbdc64d47fc35da378efe401879a_l3.png) , a niebieski to
, a niebieski to ![Rendered by QuickLaTeX.com \hkl[1 1 0]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-9e492343c5ab0c0ad76f348639e78692_l3.png) . Ciekawie zrobi się dopiero, gdy będziemy opisywać płaszczyzny w układzie heksagonalnym.
. Ciekawie zrobi się dopiero, gdy będziemy opisywać płaszczyzny w układzie heksagonalnym.
Płaszczyzny
Przejdźmy do kwintesencji wskaźników Millera, czyli opisywania płaszczyzn. Po co nam ta umiejętność? Otóż czasami światło odbite przez dwie powierzchnie w krysztale zostaje wzmocnione przez konstruktywną interferencję – nakładanie się grzbietów fal w zgodnej fazie. Możemy zmierzyć długość tak wzmocnionej fali i, znając odległość między dwiema płaszczyznami, obliczyć długości wszystkich odcinków w komórce elementarnej. Ważne jest również, że każda sieć Bravais’go posiada inny zestaw płaszczyzn, od których światło może się odbijać.
Współczynniki 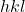 w opisie płaszczyzn oznaczają odwrotność odległości, co jaką płaszczyzna przecina osie
w opisie płaszczyzn oznaczają odwrotność odległości, co jaką płaszczyzna przecina osie 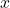 ,
, 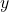 ,
,  . Definicja bardzo prosta, ale czasami trudno jest wyobrazić sobie płaszczyznę wyłącznie na podstawie tego, w jakich odległościach przecina osie. Skoro opanowaliśmy już wektory, warto zapamiętać, że wektor o danych wskaźnikach wychodzący z punktu
. Definicja bardzo prosta, ale czasami trudno jest wyobrazić sobie płaszczyznę wyłącznie na podstawie tego, w jakich odległościach przecina osie. Skoro opanowaliśmy już wektory, warto zapamiętać, że wektor o danych wskaźnikach wychodzący z punktu 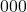 jest prostopadły do płaszczyzny o tych samych wskaźnikach.
jest prostopadły do płaszczyzny o tych samych wskaźnikach.
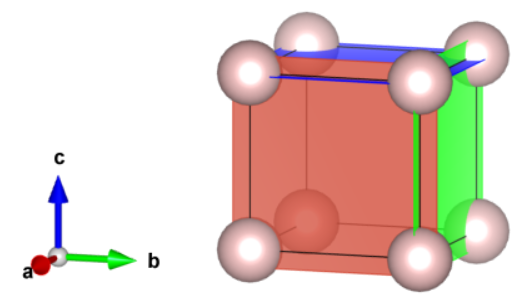
Na rys. 10. widać najprostsze płaszczyzny. Zacznijmy od czerwonej – skoro przecina oś 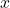 , w odległości 1, to jej parametry (które dla płaszczyzn zapisujemy w nawiasach okrągłych) wynoszą
, w odległości 1, to jej parametry (które dla płaszczyzn zapisujemy w nawiasach okrągłych) wynoszą 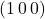 i oczywiście wektor o tych samych współrzędnych jest do niej prostopadły. Zauważmy, że gdy płaszczyzna jest równoległa do którejś osi, to odpowiadający jej współczynnik wynosi 0. Niektórzy mogą się nie zgodzić, bo akurat w naszym przypadku przecina ona osie
i oczywiście wektor o tych samych współrzędnych jest do niej prostopadły. Zauważmy, że gdy płaszczyzna jest równoległa do którejś osi, to odpowiadający jej współczynnik wynosi 0. Niektórzy mogą się nie zgodzić, bo akurat w naszym przypadku przecina ona osie 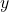 i
i  w nieskończonej ilości punktów, ale żeby zapis zawierał tylko liczby, piszemy po prostu 0.
w nieskończonej ilości punktów, ale żeby zapis zawierał tylko liczby, piszemy po prostu 0.
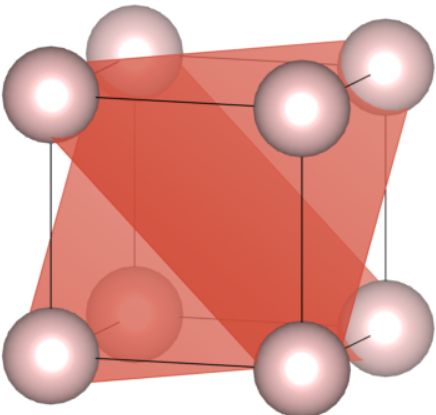
Płaszczyzny 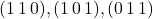 nie powinny stanowić problemu. Natomiast z płaszczyzną
nie powinny stanowić problemu. Natomiast z płaszczyzną 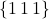 zauważamy ciekawe zjawisko – występuje ona w sieci dwukrotnie, mimo że nie ma wskaźnika większego od jeden (dlatego zapisałem wskaźniki w nawiasach klamrowych, co oznacza zbiór wszystkich płaszczyzn o tych samych wskaźnikach). Zauważ, że o ile „tylna” płaszczyzna jest jak najbardziej logiczna, to ta przednia również spełnia opis – przecina oś co jedną jednostkę, jest po prostu kolejną instancją (powtórzeniem) tej samej płaszczyzny, a niejako wychodzi z komórki przesuniętej o wektor
zauważamy ciekawe zjawisko – występuje ona w sieci dwukrotnie, mimo że nie ma wskaźnika większego od jeden (dlatego zapisałem wskaźniki w nawiasach klamrowych, co oznacza zbiór wszystkich płaszczyzn o tych samych wskaźnikach). Zauważ, że o ile „tylna” płaszczyzna jest jak najbardziej logiczna, to ta przednia również spełnia opis – przecina oś co jedną jednostkę, jest po prostu kolejną instancją (powtórzeniem) tej samej płaszczyzny, a niejako wychodzi z komórki przesuniętej o wektor ![Rendered by QuickLaTeX.com \hkl[1 0 0]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-d2e080ab49294ef5a61ea90d12d1e46a_l3.png) lub
lub ![Rendered by QuickLaTeX.com \hkl[0 1 0]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5a532a77d67c29d821bb0fc6061ef97a_l3.png) .
.
Zaznaczmy jeszcze, że jeżeli zmienimy wszystkie wartości wskaźników na przeciwne, to otrzymamy tę samą płaszczyznę. Teraz przyjrzyjmy się trudniejszym przykładom – z wartościami większymi od jeden oraz z mieszanymi liczbami dodatnimi i ujemnymi.
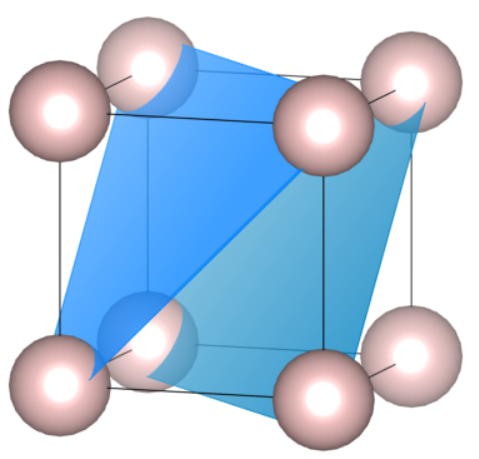
Ten przykład może być bardziej problematyczny, bo pojawia się wartość ujemna. Musimy więc wyobrazić sobie, że płaszczyzna ta przecina oś 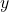 w punkcie o współrzędnej -1, czyli wyobrażamy sobie w tym przypadku dorysowaną komórkę po lewej – tam płaszczyzna, która jest na obrazku „z przodu”, przecina oś
w punkcie o współrzędnej -1, czyli wyobrażamy sobie w tym przypadku dorysowaną komórkę po lewej – tam płaszczyzna, która jest na obrazku „z przodu”, przecina oś 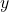 . W takim przypadku może być łatwiej wyobrazić sobie wektor prostopadły do płaszczyzny, łączący punkty
. W takim przypadku może być łatwiej wyobrazić sobie wektor prostopadły do płaszczyzny, łączący punkty  i
i 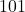 , czyli
, czyli ![Rendered by QuickLaTeX.com \hkl [1 -1 1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3b114f8b1073240307803c2e1c98d2f1_l3.png) i faktycznie, są to również wskaźniki tej płaszczyzny. W tym momencie ktoś mógłby powiedzieć, że to, czy wektor jest prostopadły, zależy wyłącznie od kierunku, a nie od zwrotu, więc tak naprawdę jest też drugi wektor o odwrotnych wskaźnikach
i faktycznie, są to również wskaźniki tej płaszczyzny. W tym momencie ktoś mógłby powiedzieć, że to, czy wektor jest prostopadły, zależy wyłącznie od kierunku, a nie od zwrotu, więc tak naprawdę jest też drugi wektor o odwrotnych wskaźnikach ![Rendered by QuickLaTeX.com \hkl[-1 1 -1]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-2257d086221f6d9b9302d986548095ad_l3.png) . Jest to oczywiście prawdziwe stwierdzenie, ale nic ono nie zmienia! Płaszczyzny te można opisać równie dobrze jako
. Jest to oczywiście prawdziwe stwierdzenie, ale nic ono nie zmienia! Płaszczyzny te można opisać równie dobrze jako 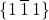 jak i
jak i 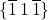 .
.
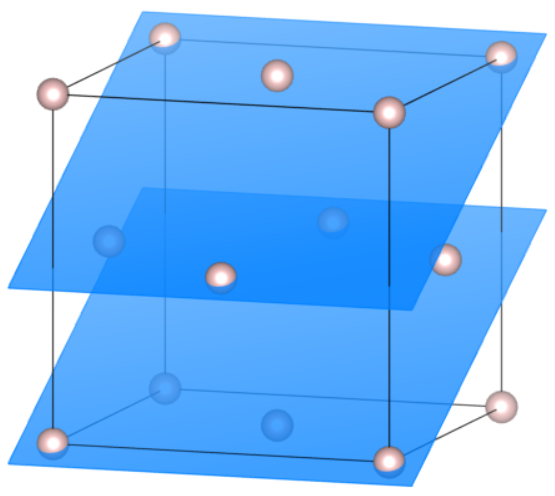
Ostatni przykład w układzie regularnym. Płaszczyzny są równoległe do osi 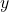 , przecinają oś
, przecinają oś 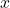 raz, co jedną jednostkę, a oś
raz, co jedną jednostkę, a oś  dwa razy, co pół jednostki. Tak więc ich wskaźniki to
dwa razy, co pół jednostki. Tak więc ich wskaźniki to 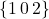 , a skoro, z definicji, przecina ona jedną oś dwukrotnie w komórce, to oczywiście występuje w niej dwukrotnie.
, a skoro, z definicji, przecina ona jedną oś dwukrotnie w komórce, to oczywiście występuje w niej dwukrotnie.
W układzie heksagonalnym opis płaszczyzn jest odrobinę bardziej skomplikowany. W celu określenia niektórych płaszczyzn potrzebny jest dodatkowy wskaźnik – 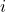 , a odpowiada on dodatkowej osi, którą definiujemy jako położoną na dwusiecznej kąta między osiami
, a odpowiada on dodatkowej osi, którą definiujemy jako położoną na dwusiecznej kąta między osiami 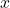 i
i 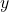 (na rysunku „a2” i „a1”). Zestaw wskaźników wypisujemy w kolejności
(na rysunku „a2” i „a1”). Zestaw wskaźników wypisujemy w kolejności 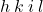 .
.
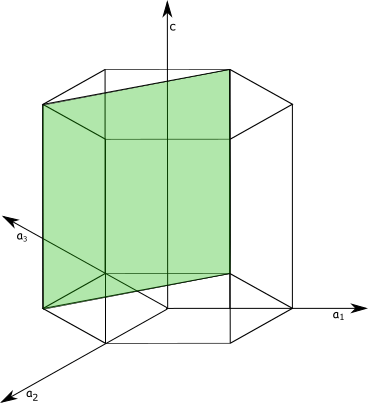
Bez zbędnego analizowania, którego było już wystarczająco dużo, bez problemu określimy tę płaszczyznę jako 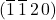 .
.
Podsumowanie
Tym sposobem wyjaśniliśmy podstawy podstaw, potrzebne do omawiania krystalografii. Wiemy, czym jest kryształ, komórka elementarna, sieć i układ krystalograficzny, centrowanie oraz wskaźniki Millera. Z taką wiedzą świetnie będzie się pracować, gdy będziemy wyprowadzać wzory, przydatne do rozwiązywania zadań na Olimpiadzie. Nie znaczy to, że to, co zawarto w tej części, jest samo w sobie nieprzydatne. Przykładowo, na II etapie 67. Olimpiady, trzeba było zaznaczyć w układzie heksagonalnym, jakie pozycje zajmowały atomy, na podstawie informacji, do której płaszczyzny są równoległe. Mogą to też się przydać, kiedy chcemy opisać strukturę kryształu, bo rysunek z polecenia Narysuj komórkę elementarną… wyszedł nam niewyraźnie.
Tak więc, nauczcie się tych podstaw (lub odświeżcie je sobie), a już niedługo zabieramy się do krystalografii z zadań olimpijskich.
Źródła i materiały:
„Introduction to Solid State Chemistry” – wykłady profesora M. J. Cima z MIT
K. Stróż, Z. Bojarski, M. Gigla, „Krystalografia”
L. Kolditz, „Chemia nieorganiczna”
Większość ilustracji wykonano przy użyciu programu VESTA – zainteresowanym serdecznie polecam sprawdzić jego możliwości, może trudno się na początku w nim połapać, ale daje ogrom możliwości.
Komentarze |0|
Tagi: Krystalografia, Matematyka, Układy krystalograficzne, Wskaźniki Millera