Kinetyka dla tych, co mają za dużo czasu: reakcje następcze
Gorąco zalecamy zapoznanie się z tekstem „Kinetyka chemiczna – wstęp” przed lekturą tego wpisu.
Reakcje następcze (consecutive reactions) to składowe reakcji wieloetapowych, czyli takich, w których występują produkty przejściowe. Aby opisać kinetykę takich procesów, rozważmy najprostszy przykład dwóch reakcji następczych pierwszego rzędu, w których 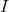 jest produktem przejściowym:
jest produktem przejściowym:
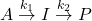
gdzie 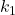 i
i 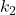 są stałymi szybkości dla odpowiednio etapu pierwszego i drugiego. Innymi słowy,
są stałymi szybkości dla odpowiednio etapu pierwszego i drugiego. Innymi słowy, 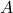 to substrat,
to substrat, 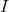 – intermediat (czyli potocznie produkt pośredni), a
– intermediat (czyli potocznie produkt pośredni), a 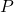 – produkt końcowy. Wszelkie poniższe wyprowadzenia przeprowadzane będą z z założeniem, że na początku reakcji mieliśmy jedynie związek
– produkt końcowy. Wszelkie poniższe wyprowadzenia przeprowadzane będą z z założeniem, że na początku reakcji mieliśmy jedynie związek 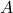 o stężeniu
o stężeniu ![Rendered by QuickLaTeX.com [\mathrm{A}]_{0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-18a49823626290ae3c09991e7c4ceb13_l3.png) . Z ostatniego wpisu wiemy już, że szybkość zaniku reagenta
. Z ostatniego wpisu wiemy już, że szybkość zaniku reagenta 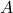 możemy określić jako:
możemy określić jako:
![Rendered by QuickLaTeX.com $$ -\frac{d[A]}{d t}=k_{1}[A] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-60beb2782e4442e021a60c2cdfa5998e_l3.png)
co po scałkowaniu można przekształcić w:
![Rendered by QuickLaTeX.com $$ [\boldsymbol{A}]=[\boldsymbol{A}]_{\mathbf{0}} \boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{1}} \boldsymbol{t}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-c04b0c98f9bf482ca18d6b54ca66afce_l3.png)
Analogicznie, powstawanie reagenta 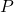 można zapisać jako:
można zapisać jako:
![Rendered by QuickLaTeX.com $$ \frac{d[P]}{d t}=k_{2}[I] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13cc0f4fe7a13bae235e09cefc899f8b_l3.png)
Wobec tego różniczka stężenia 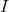 wyrażona jest równaniem:
wyrażona jest równaniem:
![Rendered by QuickLaTeX.com $$ \frac{d[I]}{d t}=k_{1}[A]-k_{2}[I] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0513790089853386dbda7248c662acf7_l3.png)
gdyż przybywa go w reakcji 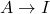 , a ubywa w reakcji
, a ubywa w reakcji 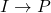 . Podstawiając scałkowaną formę pierwszego wyrażenia, otrzymujemy liniowe równanie różniczkowe pierwszego rzędu:
. Podstawiając scałkowaną formę pierwszego wyrażenia, otrzymujemy liniowe równanie różniczkowe pierwszego rzędu:
![Rendered by QuickLaTeX.com $$ \frac{d[I]}{d t}=k_{1}[A]_{0} e^{-k_{1} t}-k_{2}[I] \ $$ $$ \frac{d[I]}{d t}+k_{2}[I]=k_{1} [A]_{0} e^{-k_{1} t} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ffad6de5b24a44ffc9501131ddd24647_l3.png)
Aby wyznaczyć z tego ![Rendered by QuickLaTeX.com [\mathrm{I}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5df0c4c34ce362a53ca6795bf9c7a7e1_l3.png) , należy scałkować powyższe wyrażenie dla warunku początkowego
, należy scałkować powyższe wyrażenie dla warunku początkowego ![Rendered by QuickLaTeX.com [I]_{0}=0](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b5bb63d05faa37da460d41bd8db5b0b2_l3.png) oraz
oraz 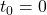 . Można to zrobić na kilka różnych sposobów, lecz my skorzystamy z podejścia zastosowanego w Chemii fizycznej K. Pigonia i Z. Ruziewicza. W podręczniku tym, tak jak i w każdym innym źródle, jakie udało mi się znaleźć, w tym miejscu wyprowadzenia autor pisze „Po scałkowaniu otrzymujemy” i podaje mniej lub bardziej gotowe wyrażenie. Sądzę, że warto wykonać te przekształcenia samodzielnie, gdyż nie dość, że wiadomo wtedy, skąd dany wzór się wziął, to jeszcze zauważy się, jeśli w podręczniku znajdzie się jakaś literówka/drobny błąd (jak np. jest w „Pigoniu”).
. Można to zrobić na kilka różnych sposobów, lecz my skorzystamy z podejścia zastosowanego w Chemii fizycznej K. Pigonia i Z. Ruziewicza. W podręczniku tym, tak jak i w każdym innym źródle, jakie udało mi się znaleźć, w tym miejscu wyprowadzenia autor pisze „Po scałkowaniu otrzymujemy” i podaje mniej lub bardziej gotowe wyrażenie. Sądzę, że warto wykonać te przekształcenia samodzielnie, gdyż nie dość, że wiadomo wtedy, skąd dany wzór się wziął, to jeszcze zauważy się, jeśli w podręczniku znajdzie się jakaś literówka/drobny błąd (jak np. jest w „Pigoniu”).
Poniższe wyprowadzenie jest dla dociekliwych – nie musicie potrafić wykonać go samodzielnie. Gdybyście jednak chcieli się tego nauczyć, polecam Rozwiązujemy zadania z analizy matematycznej T. Radożyckiego oraz Calculus M. Spivaka (po angielsku). Można też pobawić się w takie wyprowadzenia trochę wygodniej – mianowicie korzystając z Wolfram Alpha (oprogramowania online rozwiązującego różnego typu problemy matematyczne).
Zatem zaczynajmy. Na początku mnożymy przez tzw. czynnik całkujący, wynoszący w tym przypadku 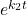 i całkując otrzymujemy:
i całkując otrzymujemy:
![Rendered by QuickLaTeX.com $$ {[I]=e^{-k_{2} t}\left(\int k_{1}[A]_{0} e^{-k_{1} t} e^{k_{2} t} d t+C\right)} \ $$ $$ \ {[I]=e^{-k_{2} t}\left(\int k_{1}[A]_{0} e^{k_{2} t-k_{1} t} d t+C\right)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-56591975a72b20b0dd71b26991ba711f_l3.png)
Robimy podstawienie 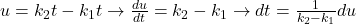 :
:
![Rendered by QuickLaTeX.com $$ [I]=e^{-k_{2} t}\left(\int k_{1}[A]_{0} \frac{1}{k_{2}-k_{1}} e^{u} d u+C\right) $$ $$ {[I]=e^{-k_{2} t}\left(k_{1}[A]_{0} \frac{1}{k_{2}-k_{1}} \int e^{u} d u+C\right)} \ $$ $$ {[I]=e^{-k_{2} t}\left(k_{1}[A]_{0} \frac{1}{k_{2}-k_{1}} \cdot \frac{e^{u}}{\ln e}+C^{\prime}\right)} \ $$ $$ {[I]=e^{-k_{2} t}\left(\frac{k_{1}[A]_{0}}{k_{2}-k_{1}} \cdot \frac{e^{u}}{1}+C^{\prime}\right)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f3692212f02fbc6c3b0edb52d6d53bb2_l3.png)
I wracamy z podstawienia:
![Rendered by QuickLaTeX.com $$ [I]=e^{-k_{2} t}\left(\frac{k_{1}[A]_{0} e^{k_{2} t-k_{1} t}}{k_{2}-k_{1}}+C^{\prime}\right) $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-76851a0ee1b0fec660812103bbb682f9_l3.png)
To było dla całki nieoznaczonej, a rozwiązujemy dla całki oznaczonej w granicach 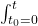 i
i ![Rendered by QuickLaTeX.com \int_{[A]_{0}=0}^{[A]}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-84dd036dee4e7f7f1a24fe0ee58216aa_l3.png) :
:
![Rendered by QuickLaTeX.com $$ {[I]=e^{-k_{2} t} k_{1}[A]_{0}\left(\frac{e^{k_{2} t}}{k_{2} e^{k_{1} t}-k_{1} e^{k_{1} t}}-\frac{1}{k_{2}-k_{1}}\right)} \ $$ $$ {[I]=e^{-k_{2} t} k_{1}[A]_{0} \frac{e^{-k_{1} t}\left(e^{k_{2} t}-e^{k_{1} t}\right)}{k_{2}-k_{1}}} \ $$ $$ {[I]=k_{1}[A]_{0} \frac{e^{-k{1} t}-e^{-k_{2} t}}{k_{2}-k_{1}}} \ $$ $$ {[\boldsymbol{I}]=[\boldsymbol{A}]_{\mathbf{0}} \frac{\boldsymbol{k}_{\mathbf{1}}}{\boldsymbol{k}_{\mathbf{2}}-\boldsymbol{k}_{\mathbf{1}}}\left(\boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{1}} \boldsymbol{t}}-\boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{2}} \boldsymbol{t}}\right)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-13743b7f6e3dd4a21c161a150ab756e4_l3.png)
Znając już chwilowe stężenia reagentów 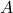 oraz
oraz 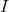 , stężenie chwilowe
, stężenie chwilowe 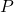 możemy obliczyć z równości:
możemy obliczyć z równości:
![Rendered by QuickLaTeX.com $$ [A]_{0}=[A]+[I]+[P] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e155ab2c274667847184b1c477290b5e_l3.png)
Nie będziemy już pokazywali wszystkich przekształceń, gdyż są one elementarne i każdy potrafi je zrobić samodzielnie.
![Rendered by QuickLaTeX.com $$ [\boldsymbol{P}]=[\boldsymbol{A}]_{\mathbf{0}}\left(\mathbf{1}-\frac{\boldsymbol{k}_{\mathbf{2}} \boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{1}} \boldsymbol{t}}-\boldsymbol{k}_{\mathbf{1}} \boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{2}} \boldsymbol{t}}}{\boldsymbol{k}_{\mathbf{2}}-\boldsymbol{k}_{\mathbf{1}}}\right) $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-1f48f0f2d46a1c9109a39058d6e9afad_l3.png)
Wykres stężeń substratu, produktu pośredniego i produktu w zależności od czasu w typowej sekwencji reakcji następczych (dla  ) wygląda następująco:
) wygląda następująco:
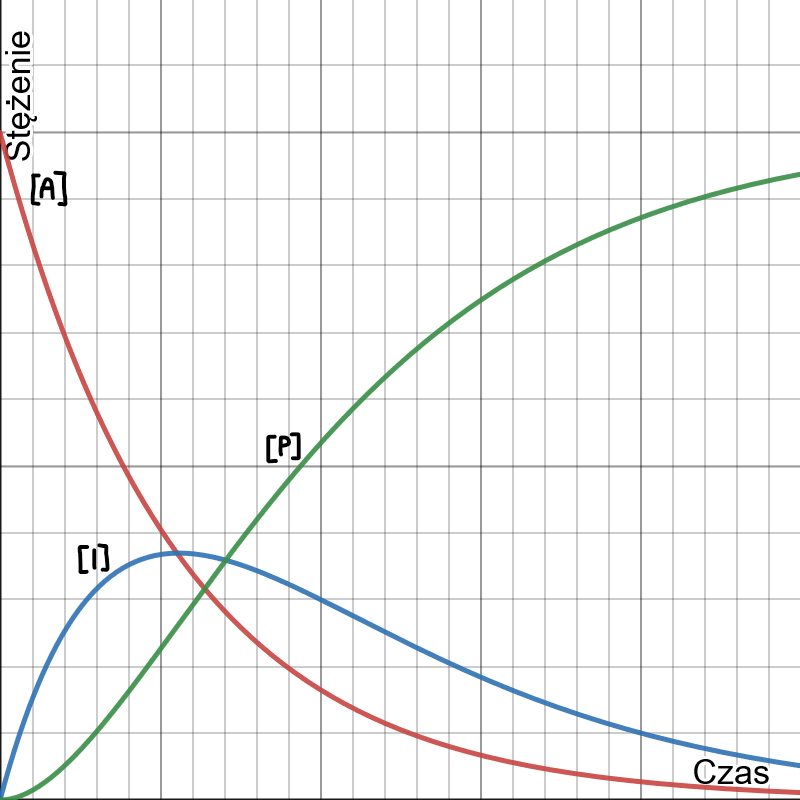
Reakcje następcze w szczególnych przypadkach
I) Na uwagę zasługuje przypadek, kiedy 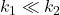 . Produkt przejściowy
. Produkt przejściowy 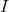 powstaje i od razu rozpada się w kolejnej reakcji. Jego stężenie jest zaniedbywalnie małe i praktycznie nie zmienia się w czasie (poniższy wykres jest dla
powstaje i od razu rozpada się w kolejnej reakcji. Jego stężenie jest zaniedbywalnie małe i praktycznie nie zmienia się w czasie (poniższy wykres jest dla  ).
).
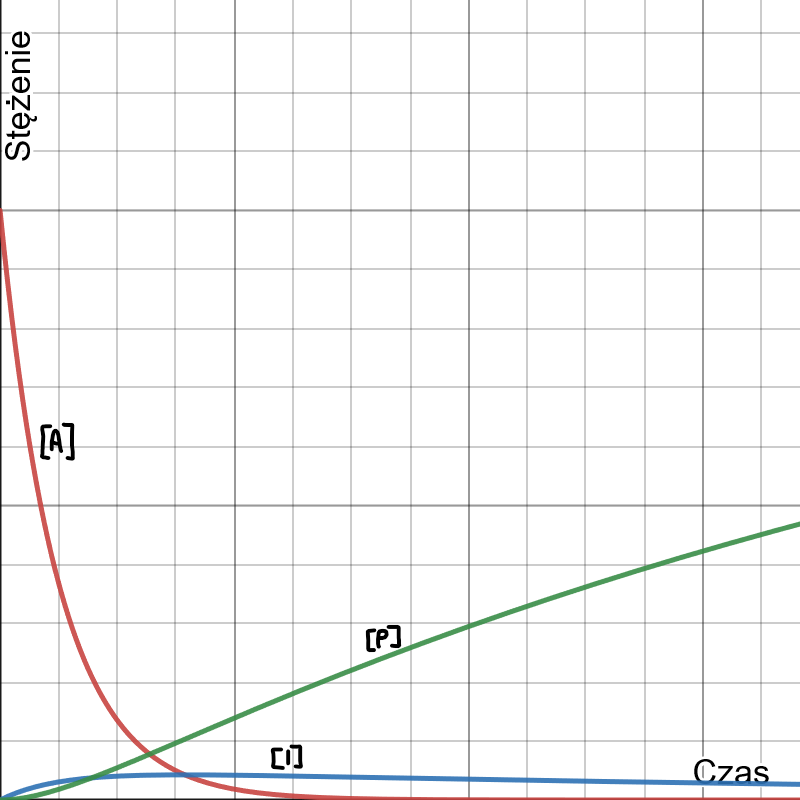
Dla uproszczenia obliczeń stosuje się wtedy tzw. przybliżenie stanu stacjonarnego, czyli założenie, że pochodna stężenia produktu pośredniego po czasie jest równa 0.
![Rendered by QuickLaTeX.com $$ \frac{d[I]}{d t} \approx 0 \ $$ $$ k_{1}[A]-k_{2}[I] \approx 0 \ $$ $$ {[I] \approx \frac{k_{1}}{k_{2}}[A]} \ $$ $$ {[I] \approx \frac{k_{1}}{k_{2}}[A]_{0} e^{-k_{1} t}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ac371680e9fa346a147ad5b50d42f8fd_l3.png)
Wobec tego:
![Rendered by QuickLaTeX.com $$ [P] \approx[A]_{0}-[A]_{0} e^{-k_{1} t}-\frac{k_{1}}{k_{2}}[A]_{0} e^{-k_{1} t} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b91fe29bcf0fb58fc93e970c5170da55_l3.png)
Przyjmujemy, że 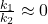 , gdyż mianownik jest dużo większy od licznika.
, gdyż mianownik jest dużo większy od licznika.
![Rendered by QuickLaTeX.com $$ {[P] \approx[A]_{0}-[A]_{0} e^{-k_{1} t}} \ $$ $$ {[\boldsymbol{P}] \approx[\boldsymbol{A}]_{\mathbf{0}}\left(\boldsymbol{1}-\boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{1}} \boldsymbol{t}}\right)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0d9c0361d9b54c9a770e60a7c2028041_l3.png)
Popularnym kryterium stosowalności przybliżenia stanu stacjonarnego jest 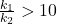 . Jego użyteczność polega przede wszystkim na tym, że zamiast rozwiązywać równanie różniczkowe, rozwiązujemy „zwykłe” równanie algebraiczne, a także na tym, że do wyznaczenia stężenia produktu końcowego potrzebujemy „dokładnej” znajomości tylko pierwszej stałej szybkości.
. Jego użyteczność polega przede wszystkim na tym, że zamiast rozwiązywać równanie różniczkowe, rozwiązujemy „zwykłe” równanie algebraiczne, a także na tym, że do wyznaczenia stężenia produktu końcowego potrzebujemy „dokładnej” znajomości tylko pierwszej stałej szybkości.
II) Gdy 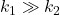 , substrat
, substrat 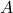 rozpada się bardzo szybko. Dopiero gdy
rozpada się bardzo szybko. Dopiero gdy ![Rendered by QuickLaTeX.com [\mathrm{I}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5df0c4c34ce362a53ca6795bf9c7a7e1_l3.png) osiąga znaczną wartość, stężenie produktu
osiąga znaczną wartość, stężenie produktu 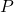 zaczyna istotnie rosnąć. W przybliżeniu rozpatrujemy reakcję jako dwa osobne etapy (poniższy wykres jest dla
zaczyna istotnie rosnąć. W przybliżeniu rozpatrujemy reakcję jako dwa osobne etapy (poniższy wykres jest dla 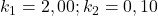 ).
).
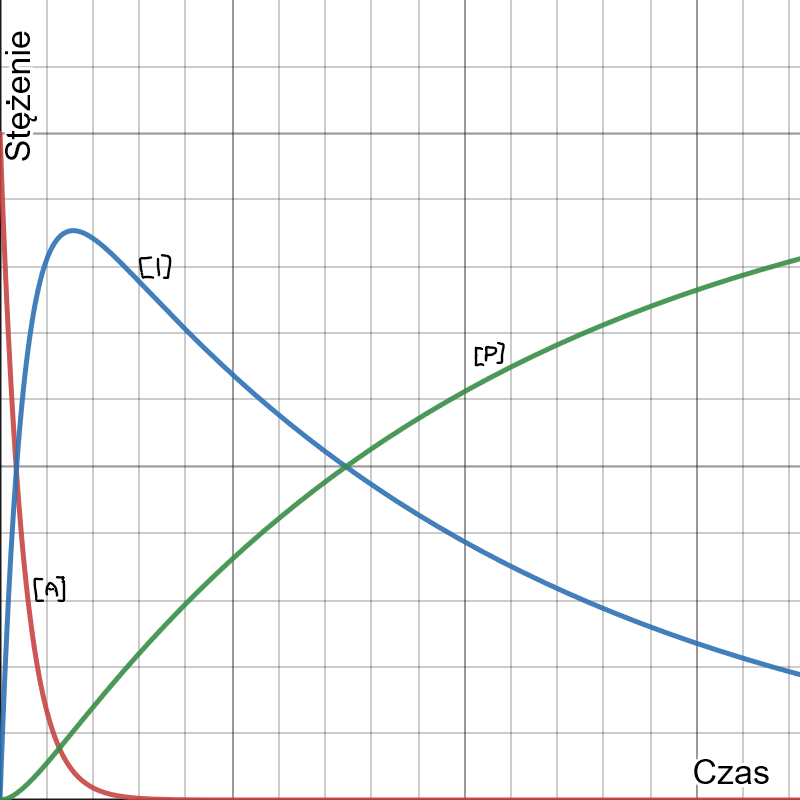
Zapiszmy jeszcze raz wzór na stężenie produktu końcowego:
![Rendered by QuickLaTeX.com $$ [P]=[A]_{0}\left(1-\frac{k_{2} e^{-k_{1} t}-k_{1} e^{-k_{2} t}}{k_{2}-k_{1}}\right) $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-fd4a11ae116b0ba9d4f5b3b6b7aae330_l3.png)
Przybliżenie w tym przypadku polega zauważeniu, że skoro 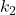 jest bardzo małe, to
jest bardzo małe, to 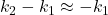 , a skoro
, a skoro 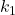 jest bardzo duże, to
jest bardzo duże, to 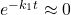 . Stosując to w równaniu, otrzymujemy:
. Stosując to w równaniu, otrzymujemy:
![Rendered by QuickLaTeX.com $$ [P] \approx[A]_{0}\left(1-\frac{-k_{1} e^{-k_{2} t}}{-k_{1}}\right)\ $$ $$ {[\boldsymbol{P}] \approx[\boldsymbol{A}]_{\mathbf{0}}\left(\boldsymbol{1}-\boldsymbol{e}^{-\boldsymbol{k}_{\mathbf{2}} \boldsymbol{t}}\right)} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-be269bfd5d67596649156210c9aee776_l3.png)
Zadanko
Związek 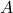 rozpada się w poniższych reakcjach następczych pierwszego rzędu:
rozpada się w poniższych reakcjach następczych pierwszego rzędu:
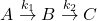
gdzie stałe szybkości wynoszą odpowiednio ![Rendered by QuickLaTeX.com k_{1}=3 \cdot 10^{-2}\left[s^{-1}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f3b6da1d84bdb5ff20440ccdc74880e7_l3.png) i
i ![Rendered by QuickLaTeX.com k_{2}=1,5 \cdot 10^{-2}\left[s^{-1}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4e10ee35fef6be8740ec1c450bafcbfd_l3.png) . Zakładając, że na początku w układzie znajdował się tylko związek
. Zakładając, że na początku w układzie znajdował się tylko związek 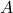 :
:
- Oblicz zawartość mieszaniny reakcyjnej 1 minutę po rozpoczęciu reakcji (w procentach molowych);
- Określ, czy stężenie produktu pośredniego wciąż wtedy rośnie, czy już maleje;
- Wyznacz maksymalne stężenie produktu pośredniego i wskaż, dla jakiego
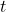 zostaje ono osiągnięte.
zostaje ono osiągnięte.

Spróbuj najpierw rozwiązać to zadanko samodzielnie
Rozwiązanie:
1. W związku z tym, że na początku w układzie był tylko związek 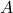 , możemy skorzystać z zależności
, możemy skorzystać z zależności ![Rendered by QuickLaTeX.com [A]_{0}=[A]+[B]+[C]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a3938d38c4c78bf631364d237c2f5ea6_l3.png) . Klasycznie, używamy równań wyznaczonych wcześniej:
. Klasycznie, używamy równań wyznaczonych wcześniej:
![Rendered by QuickLaTeX.com \%{\operatorname{mol}(A)}=\frac{[A]}{[A]+[B]+[C]}=\frac{[A]_{0} e^{-k_{1} t}}{[A]_{0}}=e^{-3 \cdot 10^{-2} \cdot 60} \approx 0,165=16,5 \%](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-425cfeee943cfdc6ca62f91d65f46e30_l3.png)
![Rendered by QuickLaTeX.com \%{\operatorname{mol}(B)}=\frac{[B]}{[A]+[B]+[C]}=\frac{[A]_{0} \frac{k_{1}}{k_{2}-k_{1}}\left(e^{-k_{1} t}-e^{-k_{2} t}\right)}{[A]_{0}} \approx 0,483=48,3 \%](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5906d184db698d49ed208dba7e198983_l3.png)
![Rendered by QuickLaTeX.com \%{\operatorname{mol}(C)}=\frac{[C]}{[A]+[B]+[C]}=\frac{[A]_{0}\left(1-\frac{k_{2} e^{-k_{1} t}-k_{1} e^{-k_{2} t}}{k_{2}-k_{1}}\right)}{[A]_{0}} \approx 0,352=35,2 \%](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-5108619c62f55b45f5de5aa90af6c711_l3.png)
2. Najłatwiej skorzystać tu z własności pochodnych funkcji. Gdy dla danego argumentu wartość pochodnej funkcji jest dodatnia, to w otoczeniu tego argumentu funkcja jest rosnąca; gdy wartość jest ujemna, to funkcja w otoczeniu danego argumentu jest malejąca, a gdy wartość pochodnej wynosi 0, to funkcja ma w tym punkcie ekstremum lokalne (maksimum bądź minimum) albo tzw. punkt przegięcia. Zapiszmy zatem wyrażenie na pochodną stężenia reagenta 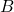 po czasie i podstawmy wyliczone w poprzednim podpunkcie dane:
po czasie i podstawmy wyliczone w poprzednim podpunkcie dane:
![Rendered by QuickLaTeX.com \frac{d[B]}{d t}=k_{1}[A]-k_{2}[B]=[A]_{0} \cdot 4,95 \cdot 10^{-3}-[A]_{0} \cdot 7,245 \cdot 10^{-3}=-2,295 \cdot 10^{-3} \cdot[A]_{0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-cb3f31cdf5c00eff85cc882285e37d84_l3.png)
Jako że ![Rendered by QuickLaTeX.com [\mathrm{A}]_{0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-18a49823626290ae3c09991e7c4ceb13_l3.png) jest zawsze dodatnie, pochodna przyjmie znak ujemny. Oznacza to, że dla
jest zawsze dodatnie, pochodna przyjmie znak ujemny. Oznacza to, że dla ![Rendered by QuickLaTeX.com t=1 [min]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b6d2924bced0081b59b610016de8bdf0_l3.png) stężenie produktu pośredniego zaczęło już maleć.
stężenie produktu pośredniego zaczęło już maleć.
Alternatywny sposób bez pochodnych: Jeśli nie umiesz jeszcze pochodnych, to możesz trochę pooszukiwać. Policz sobie po prostu wartości dla jakichś zbliżonych wartości 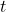 , na przykład dla
, na przykład dla ![Rendered by QuickLaTeX.com t=59,99 [s]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f7aae936ae7ec09d20c29b383de2d446_l3.png) i
i ![Rendered by QuickLaTeX.com t=60,01 [s]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-c7fe1a4e472b8b72597b35b780b5b965_l3.png) i sprawdź, jak to stężenie się zmienia. Należy pamiętać, że takie obliczenia nie są dowodem matematycznym, że funkcja jest rosnąca lub malejąca, więc nie można ich wpisać jako uzasadnienie – mogą jednak posłużyć nam jako podpowiedź.
i sprawdź, jak to stężenie się zmienia. Należy pamiętać, że takie obliczenia nie są dowodem matematycznym, że funkcja jest rosnąca lub malejąca, więc nie można ich wpisać jako uzasadnienie – mogą jednak posłużyć nam jako podpowiedź.
3. Po raz kolejny skorzystamy z pochodnej – tym razem przyrównamy ją do zera, aby wyznaczyć maksimum lokalne. Najpierw musimy przekształcić wyrażenie na nią tak, abyśmy mogli wyznaczyć z niego 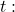
![Rendered by QuickLaTeX.com $$ \frac{d[B]}{d t}=k_{1}[A]-k_{2}[B]=0\ $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-782598a5d6dfb39623c7f42a253dd597_l3.png)
![Rendered by QuickLaTeX.com $$ \frac{d[B]}{d t}=k_{1}[A]_{0} e^{-k_{1} t_{\max }}-k_{2}[A]_{0} \frac{k_{1}}{k_{2}-k_{1}}\left(e^{-k_{1} t_{\max }}-e^{-k_{2} t_{\max }}\right)=0\ $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-fdcb00794240d6bcfa22d21e76374d1c_l3.png)
![Rendered by QuickLaTeX.com $$ \frac{d[B]}{d t}=[A]_{0} k_{1}\left(\frac{\left(k_{2}-k_{1}\right) e^{-k_{1} t_{\max }}-k_{2}\left(e^{-k_{1} t_{\max }}-e^{-k_{2} t_{\max }}\right)}{k_{2}-k_{1}}\right)=0 $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f9e9d710d83ca8ecb6a2675cb05ef29b_l3.png)
![Rendered by QuickLaTeX.com $$ \frac{d[B]}{d t}=-[A]_{0} k_{1} \frac{\left(k_{1} e^{-k_{1} t_{\max }}-k_{2} e^{-k_{2} t_{\max }}\right)}{k_{2}-k_{1}}=0 $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-8b6837d7da39bee16159f27a28cd67aa_l3.png)
Aby powyższe wyrażenie równało się 0, wyrażenie w nawiasie musi się równać 0 (gdyż ![Rendered by QuickLaTeX.com [\mathrm{A}]_{0} \neq {0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35828beda48aa6ba82933ff9861a5f78_l3.png) oraz
oraz 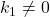 ), czyli:
), czyli:
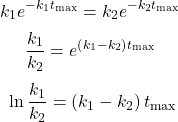
czyli:
![Rendered by QuickLaTeX.com $$ \boldsymbol{t}_{\boldsymbol{max}}=\frac{\mathbf{1}}{\boldsymbol{k}_{\mathbf{1}}-\boldsymbol{k}_{\mathbf{2}}} \cdot \boldsymbol{ln} \frac{\boldsymbol{k}_{\mathbf{1}}}{\boldsymbol{k}_{\mathbf{2}}} \approx 46,21[s] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3012eb69d9a6bae7bc1224913b3bc4b9_l3.png)
Stężenie maksymalne produktu przejściowego obliczamy już standardowo – podstawiając wyznaczone 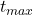 do równania na
do równania na ![Rendered by QuickLaTeX.com [\mathrm{B}]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-9159fce1c3a082a7d1334fbbf3a10277_l3.png) .
.
![Rendered by QuickLaTeX.com $$ [\mathrm{B}]_{max} \approx 0,500[\mathrm{A}]_{0} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-d48a287faa4ad80a1b4d6e1d8f9bb59e_l3.png)
Więcej poczytasz w:
- Chemii fizycznej K. Pigonia i Z. Ruziewicza;
- Chemii fizycznej P. Atkinsa („dużej” – w „małym Atkinsie” (Podstawach chemii fizycznej) tego nie ma);
- https://www.dalalinstitute.com/wp-content/uploads/Books/A-Textbook-of-Physical-Chemistry-Volume-1/ATOPCV1-3-3-Rate-Law-for-Consecutive-and-Parallel-Reactions-of-Ist-Order-Reactions.pdf (opracowanie z Dalal Institute – po angielsku);
- https://authors.library.caltech.edu/25070/5/FundChemReaxEngCh4.pdf (opracowanie po angielsku);
- https://en.wikipedia.org/wiki/Rate_equation#Consecutive_reactions;
- https://en.wikipedia.org/wiki/Steady_state_(chemistry).
Postscriptum:
Wykresy takie jak te z wpisu polecam robić w Desmosie (a testowałam kilka różnych programów). Jest niska szansa, że ta teoria pojawi się na Olchemie bez uprzedzenia, jednak jej znajomość przydaje się do zrozumienia z innych rzeczy w kinetyce, co zresztą zobaczymy w jednym z następnych wpisów.
Komentarze |1|
Tagi: III etap, Kinetyka, Matematyka, Wyprowadzenie wzorów, Zadanie we wpisie
bardzo ciekawy artykuł pozdrawiam z rodzinką