Kinetyka chemiczna – wstęp
Kinetyka chemiczna to dział, który bada szybkość oraz mechanizmy reakcji (zarówno organicznych jak i nieorganicznych). Pierwsze badania ilościowe w tej dziedzinie zostały przeprowadzone w 1850 roku przez niemieckiego chemika Ludwiga Wilhelmy’ego, którego praca dotyczyła rozkładu sacharozy na glukozę i fruktozę w środowisku kwasowym. Pod koniec XIX w. zostały sformułowane podstawowe prawa pozwalające opisać szybkość reakcji, takie jak równanie Arrheniusa oraz reguła van’t Hoffa. Badania nad mechanizmami zaczęły się dopiero później, ponieważ wymagały one udoskonalonych fizykochemicznych metod badawczych.
Szybkość reakcji określa się poprzez szybkość zmiany stężenia danego reagenta. Szybkości te zmieniają się w czasie trwania reakcji – należy zatem raczej rozważać szybkość chwilową reakcji, określoną dla konkretnego punktu w czasie. Gdy pomyślimy sobie o wyznaczeniu szybkości w określonym punkcie, możemy wpierw pomyśleć, że to niemożliwe. Bo jak? Gdy „zamrozimy” sobie czas tak, aby zatrzymać się w jednym punkcie, nie możemy mówić o ruchu, toteż o szybkości. Do takich właśnie sytuacji służy pochodna. Jej matematyczna definicja nie jest bardzo skomplikowana, lecz wymaga znajomości granic, a tym samym ciągów, więc nie będziemy się w to zagłębiali. Na nasze chemiczne potrzeby możemy przyjąć, że pochodna to taka „bardzo mała zmiana”. Możemy ją wyrazić np. „deltą” – tak jak w fizyce. Tę „deltę” – nieskończenie małą zmianę oznacza się jako „d”. Weźmy w takim razie reakcję o równaniu:
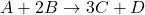
Wtedy jej szybkość możemy określić jako:
![Rendered by QuickLaTeX.com $$ v=\frac{-d[D]}{d t}=\frac{1}{3} \frac{d[C]}{d t}=-\frac{d[A]}{d t}=-\frac{1}{2} \frac{d[B]}{d t} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0101e7996d10c99c87fbe801c16818b6_l3.png)
Produktu C będzie przybywać trzy razy szybciej niż produktu D, więc trzeba ujednolicić wzór na szybkość reakcji, aby nie był on względny.
W reakcji następuje ubytek reagenta A, więc ta zmiana będzie ujemna, a szybkość nie może być ujemna, więc należy wstawić minus przed pochodną.
Wyprowadzenie z definicji
Formalnie szybkość reakcji definiuje się na podstawie „postępu reakcji” oznaczanego jako ξ (małe greckie ksi), który określa się jako:
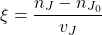
gdzie 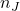 jest chwilową liczbą moli reagenta J,
jest chwilową liczbą moli reagenta J, 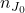 – początkową liczbą moli reagenta J, zaś
– początkową liczbą moli reagenta J, zaś 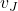 – współczynnikiem stechiometrycznym reagenta J (np. dla C w powyższej reakcji
– współczynnikiem stechiometrycznym reagenta J (np. dla C w powyższej reakcji 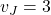 ).
).
O ile objętość układu pozostaje stała, szybkość reakcji homogenicznej (czyli zachodzącej całkowicie w obrębie jednej fazy) oficjalnie definiuje się wzorem:
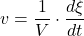
Pochodną z postępu reakcji po czasie dzielimy przez objętość – zauważmy, że jednostką szybkości jest 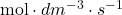 . Pochodne mają tę właściwość, że „nie zwracają uwagi” na stałe – możemy je dowolnie „dorzucać” lub wyciągać przed pochodną. Zauważmy, że
. Pochodne mają tę właściwość, że „nie zwracają uwagi” na stałe – możemy je dowolnie „dorzucać” lub wyciągać przed pochodną. Zauważmy, że 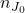 będzie stałe dla każdego momentu reakcji – możemy je zatem wyrzucić z wyrażenia na pochodną postępu reakcji po czasie. Dlatego korzystając z pierwszego równania, definicję można przekształcić w następujący sposób:
będzie stałe dla każdego momentu reakcji – możemy je zatem wyrzucić z wyrażenia na pochodną postępu reakcji po czasie. Dlatego korzystając z pierwszego równania, definicję można przekształcić w następujący sposób:
![Rendered by QuickLaTeX.com $$ v=\frac{1}{V} \cdot \frac{1}{v_{J}} \cdot \frac{d n_{J}}{d t} $$ $$v=\frac{1}{v_{J}} \cdot \frac{d[J]}{d t}$$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-c5fa23b467b53e1025a1fbf260a2b0bf_l3.png)
Tym samym otrzymujemy wzór przedstawiony na początku wpisu.
Jak mierzymy doświadczalnie szybkość reakcji?
I metoda (dla relatywnie wolnych reakcji) – reakcję inicjuje się w reaktorze poprzez zwykłe zmieszanie substratów mechanicznie (np. mieszadełkiem magnetycznym). Skład mieszaniny reakcyjnej analizuje się przez cały czas trwania reakcji bądź poprzez pobieranie niewielkich próbek co jakiś czas. Metoda ta nazywa się real-time analysis, czyli analiza w czasie rzeczywistym. Technik określania samej zawartości mieszaniny na przestrzeni czasu jest wiele, choć najczęściej używana jest spektroskopia, gdyż pozwala ona na szybki i dokładny pomiar. Gdy reagenty są w stanie gazowym, możemy mierzyć np. zmianę ciśnienia bądź objętości układu. Gdy występują związki chiralne – dobrym pomysłem jest polarymetria (technika polegająca na określaniu kąta skręcenia światła, co umożliwia wyznaczanie stężenia związku optycznie czynnego). Inne sposoby określania składu mieszaniny obejmują np. pomiar pH lub przewodnictwa w roztworze, NMR i wiele innych. Wadą tej metody jest to, że musimy założyć, że czas mieszania substratów jest zaniedbywalny, choć w rzeczywistości tak nie jest.
II metoda (dla wolnych reakcji) – badana reakcja zostaje zainicjowana, a po upływie dokładnie odmierzonego czasu „zamraża się” ją, czyli powoduje jej gwałtowne zahamowanie. Można to zrobić poprzez np. obniżenie temperatury układu do bardzo niskiej albo dodanie czynnika zobojętniającego lub dużej ilości rozpuszczalnika. Następnie pobraną próbkę bada się, oznaczając analitycznie (często przez chromatografię gazową) stężenie wybranego reagenta. Mankamentem jest tu wymóg, że reakcja musi być na tyle powolna, by można było zaniedbać jej przebieg w czasie zamrażania.
III metoda (dla szybkich reakcji) – technika przepływowa. Polega na bardzo szybkim 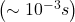 i dokładnym wymieszaniu roztworów substratów w komorze mieszania i pomiarze metodą ciągłą (np. spektroskopowo) stężeń reagentów w wypływającym z niej strumieniu. Metoda ta jest stosowana zarówno do badania reakcji gazowych, jak i szybkich reakcji w roztworach. Niedogodnością tej techniki jest jednak konieczność użycia znacznych objętości roztworów, ponieważ ich strumień musi przepływać przez aparaturę przez cały czas trwania pomiaru.
i dokładnym wymieszaniu roztworów substratów w komorze mieszania i pomiarze metodą ciągłą (np. spektroskopowo) stężeń reagentów w wypływającym z niej strumieniu. Metoda ta jest stosowana zarówno do badania reakcji gazowych, jak i szybkich reakcji w roztworach. Niedogodnością tej techniki jest jednak konieczność użycia znacznych objętości roztworów, ponieważ ich strumień musi przepływać przez aparaturę przez cały czas trwania pomiaru.
IV metoda (dla bardzo szybkich reakcji) – fotoliza błyskowa. Próbkę oświetla się krótkim błyskiem promieniowania, co powoduje inicjację procesów fotochemicznych. Przebieg reakcji śledzi się, rejestrując widmo emisyjne lub absorpcyjne w różnych odstępach od momentu błysku.
Rząd reakcji
Często okazuje się, że szybkość reakcji jest proporcjonalna do stężenia substratów. Taką proporcję określa się równaniem kinetycznym:
![Rendered by QuickLaTeX.com $$ v=k \cdot[A]^{a} \cdot[B]^{b} \cdot[C]^{c} \cdot \ldots $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-3eb06669e6a29792e17393ce3a5e11c2_l3.png)
gdzie 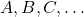 są substratami w najwolniejszym etapie reakcji;
są substratami w najwolniejszym etapie reakcji; 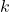 to stała szybkości reakcji.
to stała szybkości reakcji.
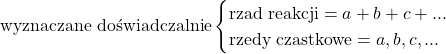
Częstym błędem podczas pisania równania kinetycznego jest zapisywanie w nim stężeń substratów reakcji podniesionych do potęgi równej współczynnikowi stechiometrycznemu danego reagenta w opisywanej reakcji. Jest to podejście nieprawidłowe, ponieważ mechanizmy reakcji, szczególnie tych nieorganicznych, są rozbudowane i w najwolniejszym etapie nie musi brać udziału akurat taka liczba cząsteczek, na jaką wskazuje sumaryczne równanie reakcji. Co więcej, rzędy cząstkowe nie muszą być nawet liczbami całkowitymi, równie dobrze mogą to być ułamki. Już raz pojawiła się taka sytuacja – w zadaniu B5 z Folderu Wstępnego 55. OlChemu. Należy o tym pamiętać, chociaż gdy w obliczeniach wychodzą nam liczby zbliżone do całkowitych, to raczej zaokrąglamy.
Wyznaczanie równania kinetycznego metodą szybkości początkowych
Badamy szybkość w chwili zmieszania substratów, zmieniając w kolejnych próbach początkowe stężenia/ciśnienia cząstkowe reagentów. Otrzymamy wtedy kilka różnych szybkości, więc możemy obliczyć zależności między nimi.
Zadanie. Metodą szybkości początkowych oblicz rzędy cząstkowe, całkowity rząd reakcji oraz stałą szybkości reakcji.
a) 
| eksperyment | ![Rendered by QuickLaTeX.com [\mathrm{ICl}]_{0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-52f352d2b9d765f4f01d242a6d7838f7_l3.png) | ![Rendered by QuickLaTeX.com \left[\mathrm{H}_{2}\right]_{0}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-dee321df093c852edc1afd5b5252f789_l3.png) | ![Rendered by QuickLaTeX.com v_{0}\left[\frac{m o l}{d m^{3} \cdot s}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-8262102dc4cd300eff09d4ddbb2e9107_l3.png) |
| 1 | 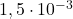 | 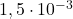 | 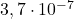 |
| 2 | 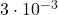 | 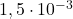 | 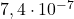 |
| 3 | 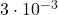 | 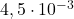 | 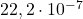 |
| 4 | 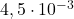 | 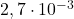 | 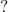 |
![Rendered by QuickLaTeX.com $$ v=k \cdot[I C l]^{a} \cdot\left[H_{2}\right]^{b} $$ $$ \frac{v_{2}}{v_{1}}=\frac{k \cdot[\mathrm{ICl}]_{2}^{a} \cdot\left[\mathrm{H}_{2}\right]_{2}^{b}}{k \cdot[\mathrm{ICl}]_{1}^{a} \cdot\left[\mathrm{H}_{2}\right]_{1}^{b}} \quad\left[\mathrm{H}_{2}\right]_{2}=\left[\mathrm{H}_{2}\right]_{1} $$ $$ 2=\frac{[I C l]_{2}^{a}}{[I C l]_{1}^{a}}=\left(\frac{[I C l]_{2}}{[I C l]_{1}}\right)^{a}=\left(\frac{3 \cdot 10^{-3}}{1,5 \cdot 10^{-3}}\right)^{a}=2^{a} $$ $$ a=1 \quad \Rightarrow \text { rząd cząstkowy względem ICl = } 1 $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-bfde3d39b0b259e33a1eda7e33c3714b_l3.png)
![Rendered by QuickLaTeX.com $$ \frac{v_{3}}{v_{2}}=\frac{k \cdot[\mathrm{ICl}]_{3}^{a} \cdot\left[\mathrm{H}_{2}\right]_{3}^{b}}{k \cdot[\mathrm{ICl}]_{2}^{a} \cdot\left[\mathrm{H}_{2}\right]_{2}^{b}} \quad\left[\mathrm{ICl}\right]_{3}=\left[\mathrm{ICl}\right]_{2} $$ $$ 3=\frac{[{H}_{2}]_{3}^{b}}{[{H}_{2}]_{2}^{b}}=\left(\frac{[{H}_{2}]_{3}}{[{H}_{2}]_{2}}\right)^{b}=\left(\frac{4,5 \cdot 10^{-3}}{1,5 \cdot 10^{-3}}\right)^{b}=3^{b} $$ $$ b=1 \quad \Rightarrow \text { rząd cząstkowy względem H2 = } 1 $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-771898c45dfa55684bc20a7930e70b20_l3.png)
Odpowiedź:
![Rendered by QuickLaTeX.com $$ \text { całkowity rząd reakcji: 2 } $$ $$ \text { równanie kinetyczne: } v=k \cdot[\mathrm{ICl}] \cdot\left[\mathrm{H}_{2}\right] $$ $$ k=\frac{v}{[I C l] \cdot\left[H_{2}\right]}=\frac{3,7 \cdot 10^{-7}}{1,5 \cdot 10^{-3} \cdot 1,5 \cdot 10^{-3}}=0,164 \frac{\mathrm{dm}^{3}}{\mathrm{~mol} \cdot \mathrm{s}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-6169104871ba0e51c1bbae81b38a5846_l3.png)
b) 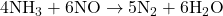
| eksperyment | ![Rendered by QuickLaTeX.com {p_{{NH_{3}}_0} [hPa]}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-fc8a1e0ff6a2115d6b142fa1bc1e21aa_l3.png) | ![Rendered by QuickLaTeX.com {p_{{NO}_0} [hPa]}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a48be1ea3d551d4847027cd09b7ca714_l3.png) | ![Rendered by QuickLaTeX.com v_{0}\left[\frac{h P a}{s}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-faf3766b6e67ce9faad90a50a915660b_l3.png) |
| 1 | 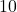 | 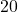 | 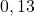 |
| 2 | 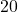 | 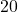 | 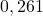 |
| 3 | 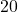 | 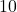 | 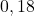 |
| 4 | 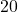 | 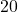 | 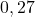 |
Pozostawiam Czytelnikowi do samodzielnego rozwiązania (nie bójcie się tych ciśnień cząstkowych – działają analogicznie do stężeń, po prostu zamiast stężenia podstawia się ciśnienie).
Wyznaczanie jednostki stałej szybkości
Jest to kolejny częsty motyw na Olimpiadzie. Łatwo zauważyć, że skoro w reakcjach różnego rzędu w równaniu kinetycznym podnosimy stężenia do różnych potęg, a szybkość reakcji zawsze ma tę samą jednostkę, to jednostka stałej szybkości reakcji musi kompensować tę różnicę. Istnieje taka zabawna sztuczka związana ze stałą. Gdy w zadaniu proszą o wyznaczenie, jakiego rzędu jest badana reakcja, czasami gdzieś w treści zapodzieje się stała szybkości tej reakcji – oczywiście z jednostką. Jako że każdy rząd ma charakterystyczną jednostkę, odpowiedź na zadane pytanie znamy już bez obliczeń.
Zadanie. Wyznacz jednostkę stałej szybkości, jeśli równanie kinetyczne ma postać:
a) ![Rendered by QuickLaTeX.com v=k \cdot[NO]^{2} \cdot\left[H_{2}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-7580d92154205b2e475629f22fb55a42_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{m o l}{d m^{3} \cdot s}\right]=k \cdot\left[\frac{m o l^{2}}{d m^{6}} \cdot \frac{m o l}{d m^{3}}\right]=k \cdot\left[\frac{m o l^{3}}{d m^{9}}\right] \quad k=\left[\frac{d m^{6}}{m o l^{2} \cdot s}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-c6901b8032d30d679d764e5cdb15c30c_l3.png)
b) ![Rendered by QuickLaTeX.com v=k \cdot\left[H_{2}\right]^{3} \cdot\left[N_{2}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-45e91a2df82cb60d7f001b4a37663ed1_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{m o l}{d m^{3} \cdot s}\right]=k \cdot\left[\frac{m o l}{d m^{9}} \cdot \frac{m o l}{d m^{3}}\right]=k \cdot\left[\frac{m o l^{4}}{d m^{12}}\right] \quad k=\left[\frac{d m^{9}}{m o l^{3} \cdot s}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b12b731497636c728152e31f4be944da_l3.png)
c) ![Rendered by QuickLaTeX.com v=k \cdot\left[\mathrm{CH}_{3} \mathrm{CHO}\right]^{\frac{3}{2}}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4c72307731274517614dc1e5c1c3360b_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{m o l}{d m^{3} \cdot s}\right]=k \cdot\left[\frac{m o l^{\frac{3}{2}}}{d m^{\frac{9}{2}}}\right] \quad k=\left[\frac{d m^{\frac{3}{2}}}{m o l^{\frac{1}{2}} \cdot s}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4e18d7059ac9dc4d03de0f97356ca273_l3.png)
Wyprowadzimy teraz wzory uzależniające stężenie substratu A od czasu oraz wzory na okresy półtrwania dla reakcji poszczególnych rzędów. [A] oznacza stężenie chwilowe w momencie t, [A0] – stężenie początkowe, k – stałą szybkości reakcji, t0 – czas początkowy (wynoszący zero), a t½ – czas półtrwania. Wiele osób uczy się tego na pamięć, a – jak pokażemy poniżej – ogarniając pochodne i całki oznaczone, co i tak przydaje się w życiu, możemy sobie bez problemu wyprowadzić każdy z tych wzorów.
Reakcja „0” rzędu
Zerowy rząd reakcji oznacza, że jej szybkość jest niezależna od stężeń substratów. Takich reakcji jest mało i są to najczęściej procesy katalityczne, takie jak rozpad katalityczny PH3 lub reakcja z katalizatorem heterofazowym, do którego może się przyłączyć ograniczona liczba cząsteczek w danym czasie.
![Rendered by QuickLaTeX.com $$ v=k \leftarrow \text { szybkość niezależna od stężeń } $$ $$ -\frac{d[A]}{d t}=k $$ $$ d[A]=-k d t $$ $$ \int_{\left[A_{0}\right]}^{[A]} d[A]=\int_{t_{0}}^{t}-k d t $$ $$ [A ]-\left[A_{0}\right]=-k t $$ $$ k t=\left[A_{0}\right]-[A] $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-f5af2b73e1617f03ae5b2e888064d08b_l3.png)
Okres półtrwania – czas, po którym ubędzie połowy substratów. Dla ![Rendered by QuickLaTeX.com t_{\frac{1}{2}},[A]=\frac{1}{2}\left[A_{0}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4083d4f10f9ad8a9fee771b25558e0dd_l3.png) .
.
![Rendered by QuickLaTeX.com $$ t_{\frac{1}{2}}=\frac{\left[A_{0}\right]}{2 k} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-d98106fdcb63004ed158c36d083d352a_l3.png)
Reakcja 1. rzędu
Do reakcji pierwszego rzędu należy na przykład rozpad promieniotwórczy.
![Rendered by QuickLaTeX.com $$ v=k[A] $$ $$ -\frac{d[A]}{d t}=k[A] $$ $$ \frac{d[A]}{d t}=-k[A] $$ $$ \frac{d[A]}{[A]}=-k d t $$ $$ \int_{\left[A_{0}\right]}^{[A]} \frac{1}{[A]} d[A]=\int_{t_{0}}^{t}-k d t $$ $$ \ln [A]-\ln \left[A_{0}\right]=-k t $$ $$ k t=\ln \frac{\left[A_{0}\right]}{[A]} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-0b91de5cdfc0005ad8ddb3da49773185_l3.png)
Reakcja pierwszego rzędu jest fenomenem – okres półtrwania nie zależy od stężenia początkowego, co zaraz wyprowadzimy. Dla ![Rendered by QuickLaTeX.com t_{\frac{1}{2}},[A]=\frac{1}{2}\left[A_{0}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4083d4f10f9ad8a9fee771b25558e0dd_l3.png) .
.
![Rendered by QuickLaTeX.com $$ -k t_{\frac{1}{2}}=\ln \frac{\frac{1}{2}\left[A_{0}\right]}{\left[A_{0}\right]} $$ $$ -k t_{\frac{1}{2}}=\ln \frac{1}{2} $$ $$ -k t_{\frac{1}{2}}=-\ln 2 $$ $$ t_{\frac{1}{2}}=\frac{\ln 2}{k} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-58b1ad279bab34d3193ddda3eca585f1_l3.png)
Reakcja 2. rzędu
Reakcjami drugiego rzędu są zazwyczaj reakcje typu 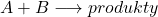 . Jeśli początkowe stężenia A i B są sobie równe, możemy przekształcić podstawowe równanie kinetyczne (
. Jeśli początkowe stężenia A i B są sobie równe, możemy przekształcić podstawowe równanie kinetyczne (![Rendered by QuickLaTeX.com v=k[A][B]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-6d061f2fa89fe00721d960aa8ef9bb85_l3.png) ) tak, jak pokazano poniżej. Jeśli stężenia te nie są równe, należy rozwiązywać wyrażenie z dwoma niewiadomymi, co staje się nieporównywalnie trudniejsze, gdy zamieszane są pochodne. Na Olchemie taka sytuacja się nie zdarzy – Komitet Główny jeszcze do tego stopnia nie zwariował, więc nie ma co się martwić. Niemniej uważam, że to wyprowadzenie jest ciekawe, więc fanów kinetyki zapraszam do wpisu „Kinetyka dla tych, co mają za dużo czasu” (coming soon). Należy też uważać na reakcję o równaniu
) tak, jak pokazano poniżej. Jeśli stężenia te nie są równe, należy rozwiązywać wyrażenie z dwoma niewiadomymi, co staje się nieporównywalnie trudniejsze, gdy zamieszane są pochodne. Na Olchemie taka sytuacja się nie zdarzy – Komitet Główny jeszcze do tego stopnia nie zwariował, więc nie ma co się martwić. Niemniej uważam, że to wyprowadzenie jest ciekawe, więc fanów kinetyki zapraszam do wpisu „Kinetyka dla tych, co mają za dużo czasu” (coming soon). Należy też uważać na reakcję o równaniu 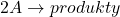 , ponieważ jej wzór na szybkość już nie będzie miał postaci
, ponieważ jej wzór na szybkość już nie będzie miał postaci ![Rendered by QuickLaTeX.com v=-d[A] \cdot d t^{-1}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b9724b2b6553c78b4c4a79173eee0f45_l3.png) , co pokazaliśmy na początku tego wpisu. To już może pojawić się na OlChemie. W każdym razie, zaczynajmy:
, co pokazaliśmy na początku tego wpisu. To już może pojawić się na OlChemie. W każdym razie, zaczynajmy:
![Rendered by QuickLaTeX.com $$ v=k[A]^{2} $$ $$ -\frac{d[A]}{d t}=k[A]^{2} $$ $$ \frac{d[A]}{[A]^{2}}=-k d t $$ $$ -\int_{\left[A_{0}\right]}^{[A]} \frac{1}{[A]^{2}} d[A]=\int_{t_{0}}^{t} k d t $$ $$ -\left|-\frac{1}{[A]}\right|_{\left[A_{0}\right]}^{[A]}=k t $$ $$ -\left(-\frac{1}{[A]}+\frac{1}{\left[A_{0}\right]}\right)=k t $$ $$ k t=\frac{1}{[A]}-\frac{1}{\left[A_{0}\right]} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-17cc3de17b2877d9611a495eabda2980_l3.png)
Okres półtrwania (jak zwykle pamiętajmy, że dla ![Rendered by QuickLaTeX.com t_{\frac{1}{2}},[A]=\frac{1}{2}\left[A_{0}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-4083d4f10f9ad8a9fee771b25558e0dd_l3.png) ):
):
![Rendered by QuickLaTeX.com $$ \frac{1}{\frac{1}{2}\left[A_{0}\right]}-\frac{1}{\left[A_{0}\right]}=k t_{\frac{1}{2}} $$ $$ 2-1=k t_{\frac{1}{2}} \cdot\left[A_{0}\right] $$ $$ t_{\frac{1}{2}}=\frac{1}{k\left[A_{0}\right]} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-24eb3af77f6b294c75b9062887ed4295_l3.png)
Reakcja n-tego rzędu
Jeżeli jednak ktoś koniecznie chce nauczyć się na pamięć sześciu wzorów powyżej, to może chociaż – zamiast uczyć się każdego z nich z osobna – nauczyć się jednego wzoru na n-ty rząd. Wzór nie działa niestety na pierwszy rząd, gdyż występuje w nim wyrażenie 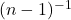 , które dla
, które dla 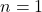 nie ma wartości rzeczywistej. Tak więc nie jest to wielka pomoc, ale i tak warto. Oczywiście obowiązuje takie samo założenie jak przy reakcji drugiego rzędu, czyli że stężenie każdego z substratów najwolniejszego etapu jest sobie równe.
nie ma wartości rzeczywistej. Tak więc nie jest to wielka pomoc, ale i tak warto. Oczywiście obowiązuje takie samo założenie jak przy reakcji drugiego rzędu, czyli że stężenie każdego z substratów najwolniejszego etapu jest sobie równe.
![Rendered by QuickLaTeX.com $$ v=k[A]^{n} $$ $$ -\frac{d[A]}{d t}=k[A]^{n} $$ $$ -\frac{d[A]}{[A]^{n}}=k d t $$ $$ -\int_{\left[A_{0}\right]}^{[A]} \frac{1}{[A]^{n}} d[A]=\int_{t_{0}}^{t} k d t $$ $$ -\left|-\frac{1}{n-1} \cdot \frac{1}{[A]^{n-1}}\right|_{\left[A_{0}\right]}^{[A]}=k t $$ $$ \frac{1}{n-1} \cdot \frac{1}{[A]^{n-1}}-\frac{1}{n-1} \cdot \frac{1}{\left[A_{0}\right]^{n-1}}=k t $$ $$ k t=\frac{1}{n-1}\left(\frac{1}{[A]^{n-1}}-\frac{1}{\left[A_{0}\right]^{n-1}}\right) $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-ace26f6f5d4346050970f68263034df3_l3.png)
Zadanka wszelakie
Taka wskazówka: Jak mamy w zadaniu sprawdzić jaki jest rząd, to najpierw podstawiamy dane do wzoru na 1. rząd, potem na 2. rząd, potem na 0. rząd, a na koniec – na 3.
Zadanie. Wykaż, że reakcja rozkładu 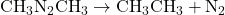 jest reakcją pierwszego rzędu mając dane:
jest reakcją pierwszego rzędu mając dane:
![Rendered by QuickLaTeX.com t[s]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-23b8649c99dfed282bd2085488cd85f4_l3.png) | 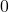 | 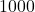 | 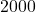 | 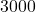 | 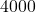 |
![Rendered by QuickLaTeX.com p_{\mathrm{CH}_{3}\mathrm{N}_{2}\mathrm{CH}_{3}}[Pa]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-e3c91f905d8a480d3d51c49dc9c54c4a_l3.png) | 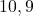 | 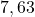 | 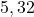 | 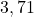 | 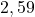 |
I metoda – sposób algebraiczny
Zauważmy, że stała szybkości reakcji jest taka sama dla każdego jej momentu. Przypomnijmy sobie wzór wiążący stężenie/ciśnienie cząstkowe z czasem dla pierwszego rzędu:
![Rendered by QuickLaTeX.com $$ k t=\ln \frac{\left[A_{0}\right]}{[A]} $$ $$ k=\frac{\ln \frac{\left[A_{0}\right]}{[A]}}{t} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-320254b3e2193b631ca4c5dedcb9d36e_l3.png)
Jeśli reakcja rzeczywiście jest pierwszego rzędu, to zachodzi równość:
![Rendered by QuickLaTeX.com $$ \frac{\ln \frac{\left[A_{0}\right]}{\left[A_{1}\right]}}{t_{1}}=\frac{\ln \frac{\left[A_{0}\right]}{\left[A_{2}\right]}}{t_{2}}=\frac{\ln \frac{\left[A_{0}\right]}{\left[A_{3}\right]}}{t_{3}}=\frac{\ln\frac{\left[A_{0}\right]}{\left[A_{4}\right]}}{t_{4}} $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-b8caca233c18c91f063b4ba7be129521_l3.png)
Wydaje się, że to dużo liczenia, prawda? Metodą na skróty jest porównanie pierwszego i ostatniego pomiaru, ponieważ teoretycznie to między nimi powinny się pojawić największe różnice w wartości stałej, o ile nie mielibyśmy racji co do swoich przypuszczeń na temat rzędu badanej reakcji.
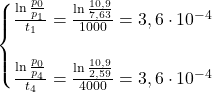
Odpowiedź: Reakcja ta jest pierwszego rzędu.
II metoda – sposób graficzny
Spójrzmy jeszcze raz na wzór wiążący stężenie/ciśnienie cząstkowe z czasem dla reakcji pierwszego rzędu:
![Rendered by QuickLaTeX.com $$ \ln \frac{\left[A_{0}\right]}{[A]}=k t $$ $$ f(x)=a x $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-9de7fbf79e740e0f03df2c431563bc97_l3.png)
Nietrudno jest zauważyć analogię do funkcji liniowej. Stała szybkości, jak sama nazwa wskazuje, jest stała dla każdego momentu reakcji, więc będzie ona naszym odpowiednikiem współczynnika  . Dlaczego wykres tej funkcji będzie liniowy jedynie gdy podstawimy dane doświadczalne z reakcji pierwszego rzędu? To proste – jak już udowodniliśmy powyżej, każdy rząd ma charakterystyczną zależność między czasem a stężeniem, więc wykorzystując dane w niepasującym (tj. niezgadzającym się z tym rzeczywistym) wzorze, wartość
. Dlaczego wykres tej funkcji będzie liniowy jedynie gdy podstawimy dane doświadczalne z reakcji pierwszego rzędu? To proste – jak już udowodniliśmy powyżej, każdy rząd ma charakterystyczną zależność między czasem a stężeniem, więc wykorzystując dane w niepasującym (tj. niezgadzającym się z tym rzeczywistym) wzorze, wartość 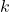 będzie się zmieniać dla każdego pomiaru. Spowoduje to „wykrzywienie się” wykresu.
będzie się zmieniać dla każdego pomiaru. Spowoduje to „wykrzywienie się” wykresu.
Tak więc: Obliczamy ![Rendered by QuickLaTeX.com \ln \frac{\left[A_{0}\right]}{\left[A_{1}\right]}, \ln \frac{\left[A_{0}\right]}{\left[A_{2}\right]}, \ln \frac{\left[A_{0}\right]}{\left[A_{3}\right]}, \ln \frac{\left[A_{0}\right]}{\left[A_{4}\right]}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-a46cdfce53753fabae3d020669ba51d1_l3.png) i robimy wykres.
i robimy wykres.
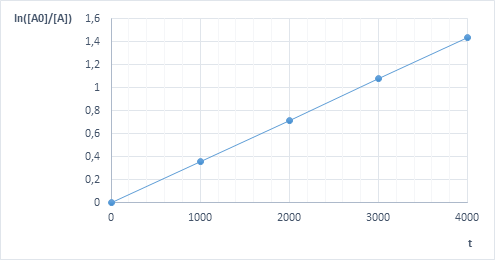
Odpowiedź: Wychodzi funkcja liniowa, więc reakcja jest pierwszego rzędu.
Zostańmy jeszcze chwilkę przy metodzie graficznej. Da się ją zastosować dla każdego rzędu reakcji. Pokażmy zatem jak to się robi.
Dla 2. rzędu:
![Rendered by QuickLaTeX.com $$ \frac{1}{[A]}-\frac{1}{\left[A_{0}\right]}=k t $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-46e923ac1c843a1e6e5a4aaeaa0dd0e4_l3.png)
Zauważmy, że wyrażenia ![Rendered by QuickLaTeX.com \left[A_{0}\right]^{-1}](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-9a3290f5e2628ac37e94e2a23a2fa9a0_l3.png) oraz oczywiście
oraz oczywiście 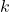 są stałe dla każdego momentu reakcji, co pozwala na analogię:
są stałe dla każdego momentu reakcji, co pozwala na analogię:
![Rendered by QuickLaTeX.com $$ \frac{1}{[A]}=k t+\frac{1}{\left[A_{0}\right]} $$ $$ f(x)=a x+b $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-51ce3d7309a507aa4aec10a019666151_l3.png)
Dla zerowego rzędu:
![Rendered by QuickLaTeX.com $$ [A]-\left[A_{0}\right]=-k t $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-bc6656c54c76de159df5f86bdba08d35_l3.png)
W każdym momencie reakcji ![Rendered by QuickLaTeX.com \left[A_{0}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-74fe5add7f98d793d1679c967ac65d69_l3.png) oraz
oraz 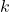 są stałe, toteż:
są stałe, toteż:
![Rendered by QuickLaTeX.com $$ [A]=-k t+\left[A_{0}\right] $$ $$ f(x)=a x+b $$](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-119511bcf669e4a85d07270f755eb1b5_l3.png)
Załóżmy więc, że narysowaliśmy już wykres i stwierdziliśmy, którego rzędu jest reakcja. Często w zadaniu pytają się od razu również o inne parametry (stałą itd.). Jak je wyznaczyć? Na pierwszy rzut oka – metodą algebraiczną. Wiedząc już do którego wzoru podstawić, wyliczamy szukane wartości dla poszczególnych pomiarów i robimy z nich średnią. Posiadając Olchemowy kalkulator Casio fx-991CEX możemy ominąć te obliczenia poprzez użycie regresji liniowej. Pokrótce: jest to metoda dopasowująca prostą lub krzywą do podanego zestawu danych. Najczęściej przyporządkowywana jest funkcja liniowa, ale możemy wybrać równie dobrze inne funkcje. Narzędzie to pozwala na wyznaczenie z relatywnie dużą dokładnością współczynników  i
i 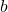 , które z kolei przekładają się na nasze szukane, jak pokazaliśmy przed chwilą. Niektórzy zawodnicy idą z użyciem regresji dalej – wcale nie rysują wykresów, a to, czy wyznaczona funkcja rzeczywiście jest liniową, oceniają na podstawie tzw. współczynnika korelacji liniowej Pearsona (oznaczanego jako rxy). Jest to podejście błędne, gdyż to kryterium często bywa zawodne. Dobrze obrazuje to poniższy przykład – współczynniki korelacji liniowej w obu przypadkach są identyczne bądź bardzo podobne:
, które z kolei przekładają się na nasze szukane, jak pokazaliśmy przed chwilą. Niektórzy zawodnicy idą z użyciem regresji dalej – wcale nie rysują wykresów, a to, czy wyznaczona funkcja rzeczywiście jest liniową, oceniają na podstawie tzw. współczynnika korelacji liniowej Pearsona (oznaczanego jako rxy). Jest to podejście błędne, gdyż to kryterium często bywa zawodne. Dobrze obrazuje to poniższy przykład – współczynniki korelacji liniowej w obu przypadkach są identyczne bądź bardzo podobne:
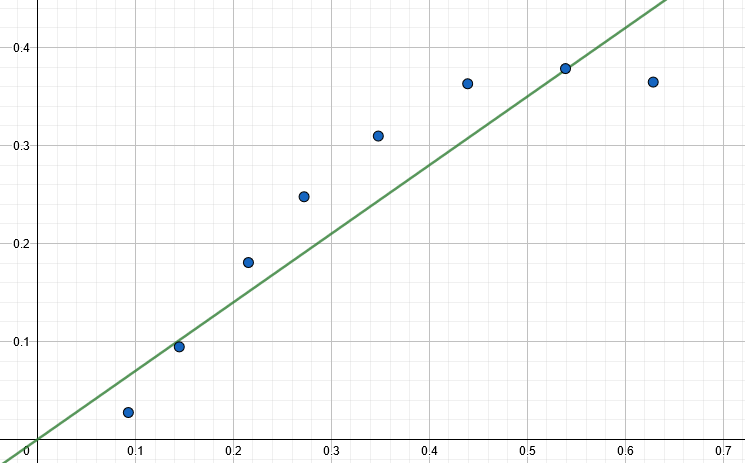
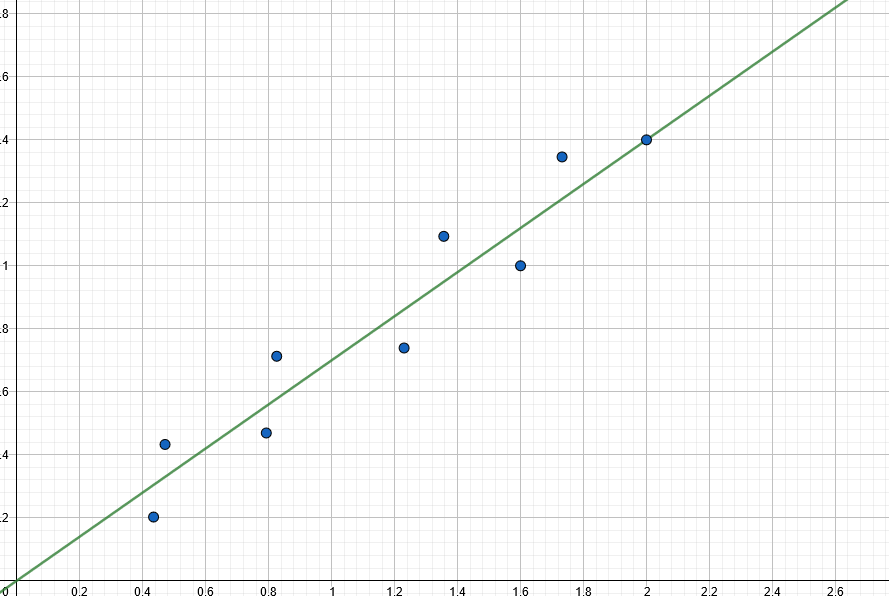
Niestety, od tegorocznej edycji Olimpiady Komitet Główny uparł się, by na drugim etapie były rozdawane słabsze kalkulatory, które – eufemizując – utrudniają wszystkim pracę, gdyż nie posiadają kilku kluczowych funkcji, od których większość zaawansowanych zawodników się już lekko uzależniła. Na szczęście regresja liniowa wciąż jest dostępna.
Zadanie. A teraz znów przykład do rozwiązania dla Was. Wykorzystajcie obie metody, to poćwiczycie. Wyznacz rząd oraz stałą szybkości reakcji o równaniu 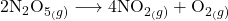 , mając do dyspozycji dane:
, mając do dyspozycji dane:
![Rendered by QuickLaTeX.com t[\min ]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-aed740673e437d7d962bbd9d9056c0a2_l3.png) | 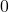 | 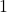 | 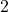 | 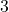 | 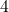 | 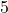 |
![Rendered by QuickLaTeX.com \left[\mathrm{N}_{2}\mathrm{O}_{5}\right]\left[\frac{\mathrm{mol}}{d m^{3}}\right]](https://allchemicznie.com/wp-content/ql-cache/quicklatex.com-35ce21ec6b175fc5f94f2db24c7790cd_l3.png) | 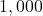 | 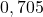 | 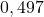 | 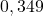 | 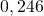 | 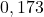 |
Zadanka z olchemu po lekturze tego wpisu
Łatwiejsze:
- Zad. A1-FW-65;
- Zad. 3-I-49;
- Zad. B1-FW-65;
- Zad A1-FW-49 (ono jest z kinetyki w rozpadach promieniotwórczych – na spokojnie będziecie potrafili je zrobić, ale będzie jeszcze o tym temacie osobny wpis).
Średnie:
- Zad. 1-I-65 (metoda szybkości początkowych);
- Zad. 1-II-65 (metoda graficzna).
Trudniejsze:
- Zad. 1-III-65 (trzeba umieć samemu wyprowadzać wzory z tych pochodnych);
- Zad. B4-FW-59 (kinetyka procesów katalitycznych);
- Zad. 3-II-59 (serio trudne; nie dacie rady go zrobić po samym tym artykule).
Komentarze |1|
Tagi: Kinetyka, Matematyka, Rząd reakcji, Stała szybkości, Wyprowadzenie wzorów
Bardzo ładnie